Questions with Answers, Solution | Numbers | Chapter 1 | 8th Maths - Exercise 1.7 | 8th Maths : Chapter 1 : Numbers
Chapter: 8th Maths : Chapter 1 : Numbers
Exercise 1.7
Exercise 1.7
Miscellaneous
Practice Problems
1. If 3/4 of a box of apples weighs 3 kg and 225 gm, how much does a full box of apples weigh?

Solution:
Let the total weight of a box of apple = x kg.
Weight of 3/4 of a box apples = 3 kg 225 gm.
= 3.225 kg
(3/4) × x = 3225
x = { [3.225 × 4] / 3 } kg = [1.075 ×
4 ] kg = 4.3 kg
= 4 kg 300 gm.
Weight of the box of apples = 4 kg 300 gm.
2. Mangalam buys a water jug of capacity 3 (4/5) litre. If she buys another
jug which is 2 (2/3) times as large as the smaller jug, how
many litre can the larger one hold?
Solution:
Capacity of the small water jug = 3 4/5 litres.
Capacity of the big jug = 2 2/3 times the small one.
= 2(2/3) × 3(4/5) = [8/3] × [19/5] = 152/15 = 
= 10 (2/15) litres
Capacity of the large jug = 10 2/15 litres =  litres.
litres.
3. Ravi multiplied 25/8 and 16/15 and he says that the simplest form of this
product is 10/3 and Chandru says the answer in the simplest
form is 3 1/3 Who is correct? (or) Are they both correct? Explain.
Solution:

Product of 25/8 and 16/15 = [25/8] × [16/15]
= 10/3 = 3 (1/3)
Answer obtained = 400/120
= [400 ÷ 40] / [120 ÷ 40] = 10/3 = 3 (1/3)
∴ The product is 400/120 and its simplest form improper fraction
is 10/3.
And mixed fraction is 3 (1/3).
∴ Both are correct.
4. Find the length of a room whose area
is 153/10 sq.m and whose breadth is 2
11/20 m.
Solution:

Length of the room × Breadth = Area of the room
Breadth of the room = 2 (11/20) m
Area of the room = 153/10 sq.m
Length × 2(11/20) = 153/10
Length = [153/10] ÷ [2 (11/20)] = 153/10 ÷ 51/20 = 153/10 × 20/51
= 6 m
Length of the room = 6 m
5. There is a large square portrait of
a leader that covers an area of 4489 cm2.
If each side has a 2 cm liner, what would
be its area?
Solution:
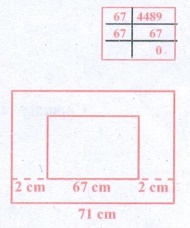
Area of the square = 4489
cm2
(side)2 = 4489
cm2
(side)2 = 67 ×
67
side2 = 672
Length of a side = 67
Length of a side with liner = 67 + 2 + 2 cm
= 71 cm
Area of the larger square = 71 × 71 cm2
= 5041 cm2
Area of the liner = Area of big square − Area of small square
= (5041 − 4489) cm2
= 552 cm2
6. A greeting card has an area 90 cm2. Between what two whole numbers
is the length of its side?
Solution:
Area of the greeting card = 90 cm2
(side)2 = 90 cm2
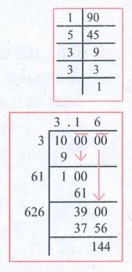
(side)2 = 2 × 5 × 3 × 3 = 2 × 5 × 32
√(side)2 = √(2×5×32)
side = 3
√(2×5)
side = 3 √10 cm
side = 3 × 3.2 cm
side = 9.6 cm
∴ Side lies between the
whole numbers 9 and 10.
7. 225 square shaped mosaic tiles, each
of area 1 square decimetre exactly cover a square shaped verandah. How long is each
side of the square shaped verandah?
Solution:
Area of one tile = 1 sq.decimeter
Area of 225 tiles = 225 sq.decimeter
225 square tiles exactly covers the square shaped verandah.
∴ Area of 225 tiles = Area of the verandah
Area of the verandah = 225 sq.decimeter
side × side = 15 × 15 sq.decimeter
side = 15 decimeters
Length of each side of verandah = 15 decimeters.
8. If 3√1906624 × √x = 3100, find x.
Solution:

9. If 2m-1 + 2m+1 = 640,
then find m.
Solution:
Given 2m−1 + 2m+1
= 640
2m−1 + 2m+1
= 128 + 512 [consecutive powers of 2]
2m−1 + 2m+1
= 27 + 29
m – 1 = 7
m = 7 + 1
m = 8
Powers of 2
2,4,8,16,32,64,128,256,512,…
10. Give the answer in scientific notation:
A human heart beats at an average of
80 beats per minute. How many times does it beat in i) an hour? ii) a day? iii)
a year? iv) 100 years?
Solution:
Heart beat per minute = 80 beats
(i) an hour
One hour = 60 minutes
Heart beat in an hour = 60 × 80
= 4800 = 4.8 × 103
(ii) In a day
One day = 24 hours = 24 × 60 minutes
∴ Heart beat in one day = 24 × 60 × 80 = 24 × 4800 = 115200
= 1.152 × 105
(iii) a year
One year = 365 days = 365 × 24 hours = 365 × 24 × 60 minutes
Heart beats in a year = 365 × 24 × 60 × 80
= 42048000 = 4.2048 × 107
(iv) 100 years
Heart beats in one year = 4.2048 × 107
Heart beats in 100 years = 4.2048 × 107 × 100 =
4.2048 × 107 × 102
= 4.2048 × 109
Challenging Problems
11. In a map, if 1 inch refers to 120
km, then find the distance between two cities B and C which are 4(1/6) inches and
3(1/3) inches from the city A which lies between the cities B and C.
Solution:

1 inch =120 km
Distance between A and B = 4 (1/6) inches
Distance between A and C = 3 (1/3) inches
∴ Distance between B and C = 4 (1/6) + 3 (1/3) inches
= 25/6 + 10/3 = 25/6 + 20/6 = [25 + 20] / 6 = 45/6 inches
1 inch = 120 km
∴ 45/6 inches = [45/6] × 120 km = 900 km
Distance between B and C = 900 km
12. Give an example and verify each of
the following statements
(i) The collection of all non-zero rational
numbers is closed under division.
(ii) Subtraction is not commutative for
rational numbers.
(iii) Division is not associative for
rational numbers.
(iv) Distributive property of multiplication
over subtraction is true for rational numbers. That is, a (b − c ) = ab
− ac .
(v) The mean of two rational numbers
is rational and lies between them
Solution:


(i) Let a = 5/6 and b
= −4/3 be two non zero rational numbers.
a ÷ b = 5/6 ÷ −4/3 = 5/6
× 3/−4 = 5/−8 is in Q
∴ Collection of non−zero rational numbers are closed under division.
(ii) Let a = 1/2 and b
= −5/6 be two rational numbers.
a – b = 1/2 − (−5/6) = 1/2 + (+5/6) = 3/6 + 5/6 = [3 + 5]
/ 6 = 8/6
= 1 (2/6)
= 1 1/3
b – a = −5/6 – 1/2 = −5/6 – 3/6 = [−5
−3] / 6 = −8/6 = −1 (1/3)
a − b
≠ b − a
∴ Subtraction is not commutative for
rational numbers.
(iii) Let a = 2/5, b
= 6/5, c = 3/5 be
three rational numbers.
a ÷ (b ÷ c) = 2/5 ÷ (6/5
÷ 3/5) = 2/5 ÷ (6/5 × 5/3)
= 2/5
÷ 2/1 = 2/5 × 1/2 = 1/5 ……….(1)
(a
÷ b) ÷ c = (2/5 ÷ 6/5) ÷ 3/5
= (2/5
× 5/6) ÷ 3/5 = 1/3 ÷ 3/5 = 1/3 × 5/3 = 5/9 ……..(2)
From
(1) and (2) 1/5 ≠ 5/9
a ÷ (b ÷ c) ≠ (a ÷
b) ÷ c
∴ Division is not associative for rational numbers.
(iv) Let a = 2/9, b
= 3/6 , c = 1/3 be three rational numbers
To
prove a × (b − c) = ab − ac
a × (b − c) = 2/9 × (3/6
− 1/3)
= [2/9]
× ( [3 − (1 × 2)] / 6 ) = [2/9] × [(3 – 2) / 6]
= 2/9
× 1/6 = 1 / 27 ……..(1)
ab − ac = (2/9 × 3/6) –
(2/9 × 1/3) = 1/9 – 2/27
= [(1
× 3) – 2] / 27 = [3 – 2] / 27 = 1/27
….(2)
∴ From (1) and (2)
a × (b − c) = ab
− ac.
∴ Distributivity of multiplication over subtraction is true for
rational numbers.
(v) Let a = 2/11 and b = 5/6 be two rational numbers.
Mean of a and b is c =1/2 (a + b) = 1/2 (2/11 + 5/6) = 1/2 ((2×6)
+ (5×11) / 66)
= 1/2 × ([12 + 55] / 66) = 1/2 × 67/66 = 67/132 is in Q.
Also 2/11 = [2 × 12] / [11 × 12] = 24/132
5/6 = [5 × 22] / [6 × 22] = 110 / 132
∴ 24/132 < 67/132 < 110/132
∴ The mean lies between the given rational numbers 2/11 and 5/6.
13. If 1/4 of a ragi adai weighs 120 grams, what will be the weight of 2/3 of the same
ragi adai?
Solution:
Let the weight of 1 ragi adai = x grams
given 1/4 of x = 120 gm
(1/4) × x = 120
x = 120 × 4
x = 480 gm
∴ 2/3 of the adai = 2/3 × 480
gm = 2 × 160 gm = 320 gm
2/3 of the weight of adai = 320 gm
14. If p + 2q = 18 and pq = 40 , find 2/p + 1/q
Solution:
Given: p + 2q = 18 ….(1)
pq = 40 ….(2)
2/p + 1/q = [(2 × q) + (l × p)] / pq
= [2q + p ] / pq = 18/40 [∵ from (1) and (2)]
2/p + 1/q = 9/20
15. Find x if 5(x/5) × 3(3/4)
= 21.
Solution:
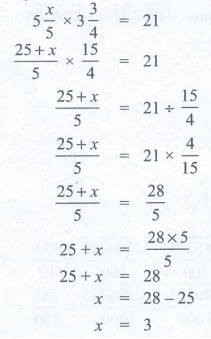
[ 5 x/5 ] × [3 3/4] = 21
[(25 + x)
/ 5] × [15/4] = 21
[ 25+ x ] /
5 = 21 ÷ [15/4]
[25+ x ] /
5 = 21 × [4/15]
[25+ x ] /
5 = 28/5
25 + x = [28 × 5] / 5
25 + x = 28
x = 28 – 25
x = 3
16. By how much does 1/(10/11) exceed
(1/10) / 11 ?
Solution:
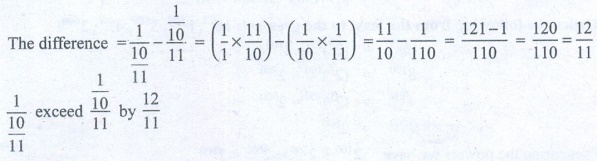
The difference = { 1 / [10/11] } – { [1/10] / 11 } = (1/1 × 11/10)
– (1/10 × 1/11) = 11/10 – 1/110 = [121 – 1] / 110 = 120/110 = 12/11
{ 1 / [10/11] } exceed {
[1/10] / 11 } by 12/11
17. A group of 1536 cadets wanted to
have a parade forming a square design. Is it possible? If it is not possible, how
many more cadets would be required?
Solution:
Number of cadets to form square design
1536 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
× 2 × 3
The numbers 2 and 3 are unpaired
∴ It is impossible to have the parade forming square design with
1536 cadets.
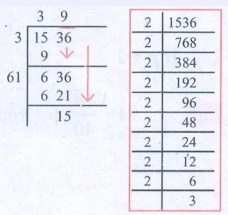
39 × 39 = 1521
Also 40 × 40 = 1600
∴ We have to add (1600 − 1536) = 64 to make 1536 a perfect
square.
∴ 64 more cadets would be
required to form the square design.
18. Evaluate: √286225 and use it to compute
√2862.25 + √28.6225
Solution:

√286225 = 535
√2862.25 = √[286225 / 100] = √286225 / √100 = 535/10 = 53.5
√28.6225 = √[286225 / 1000] = √286225/√10000 = 535/100 = 5.35
∴ √2862.25 + √28.6225 = 53.5 + 5.35 = 58.85
19. Simplify: (3.769 × 105) + (4.21 × 105)
Solution:

(3.769 × 105) + (4.21 × 105) =
3,76,900 + 4,21,000
= 7,97,900 = 7.979 × 105
20. Order the following from the least
to the greatest: 1625 , 8100 , 3500 , 4400
, 2600
Solution:
1625 = (24)25 = 2100
8100 = (23)100
= 2300
4400 = (22)400 = 2800
2600 = 2600
Comparing the powers we have. 2100 < 2300
< 2600 < 2800
∴ The required order : 1625 , 8100, 2600,
3500, 4400
Exercise
1.7
Miscellaneous Practice
Problems
1. 4 kg 300 gm
2. 10 2/5 litre
3. both are correct
4. 6 m
5. 552 cm2
6. 9 cm and 10 cm
7. 15 decimetre
8. 625
9. 8
10. (i) 4.8 × 103
(ii) 1.152 × 105 (iii) 4.2048 × 107 (iv) 4.2048 × 109
Challenging Problems
11. 900 km
13. 320 gm
14. 9/20
15. x = 3
16. 12/11
17. No, 64
18. 58.85
19. 7.979 × 105
20. 8100, 2600,
3500, 4400, 1625
Related Topics