Numbers | Chapter 1 | 8th Maths - Comparison of rational numbers | 8th Maths : Chapter 1 : Numbers
Chapter: 8th Maths : Chapter 1 : Numbers
Comparison of rational numbers
Comparison
of rational numbers
It is useful
to remember the following points:
• Every positive
number is greater than zero.
• Every negative
number is smaller than zero.
• Every positive
number is greater than every negative number.
• Every number
on the right of a number on a number line is greater than that number.
When two
integers or fractions are given, we know how to compare them and say which is greater
or smaller. Now, in the same way, we can compare a pair of rational numbers.
Type 1 : Comparing two
rational numbers with opposite signs
Example 1.3
Compare 5/17
and -10/19.
Solution:
Since every
positive number is greater than every negative number, we conclude that 5/17 >
-10/19.
Type 2 : Comparing two
rational numbers represented by two fractions with same denominators
Example 1.4
Compare 1/3
and 4/3.
Solution:
Since the
denominators are the same, just compare the numerators.
Since 1 <
4, we conclude that 1/3 < 4/3.
Type 3 : Comparing two
rational numbers represented by two fractions with different denominators
Example 1.5
Compare
3/4 and 5/6.
Solution:
The LCM of the denominators is 12 (Find it!). Consider for each rational number an equivalent rational number with the LCM 12 as denominator
We get
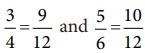
3/4 = 9/12 and 5/6 =
10/12, which become like fractions now.
Here, 9/12 < 10/12. Hence,
we conclude that 3/4 < 5/6.
Type 4 : Comparing two
rational numbers that are not in standard form
Example 1.6
Compare 9/-4 and -2/3.
Solution:
The
number 9/-4 is not in standard form. First put it in the standard form.

Now,
we shall compare the fractions -9/4 and -2/3. We find that these two fractions are
unlike fractions. To make them as like fractions, we make use of their LCM, which
is 12.
We
can now compare their equivalent fractions -9/4 = -27/12 and -2/3 = -8/12 (How?)
We
find that the denominators are the same and so just comparing the numerators –27
and –8 are enough Visualizing these numbers on the number line, we see that
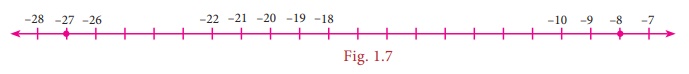
–8 is to the right of –27 and hence (–8) > (–27).
This leads to the result that -8/12 > -27/12 and consequently we conclude that
-2/3 > 9/-4 .
Example 1.7
Write the
following rational numbers in ascending and descending order.
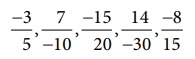
Solution:
First
make the denominators to be positive and write the numbers in standard form as 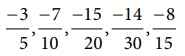 . Here, the LCM of 5,10,15,20 and 30
is 60 (Find it!). Change the given rational numbers in equivalent form with common
denominator 60.
. Here, the LCM of 5,10,15,20 and 30
is 60 (Find it!). Change the given rational numbers in equivalent form with common
denominator 60.
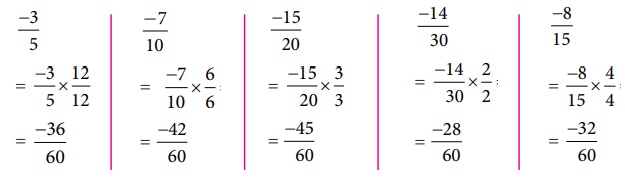
Comparing
the numerators alone, that is, −36, −42, −45, −28 and –32 we see that
−45 < −42 < −36 < −32 < −28
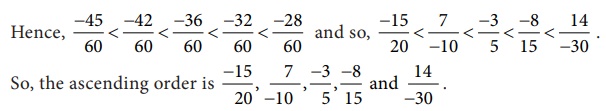
Also, its
reverse order gives the descending order as 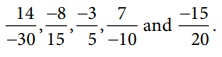
Related Topics