Numbers | Chapter 1 | 8th Maths - Cubes and Cube Roots | 8th Maths : Chapter 1 : Numbers
Chapter: 8th Maths : Chapter 1 : Numbers
Cubes and Cube Roots
Cubes and
Cube Roots
If you multiply
a number by itself and then by itself again, the result is a cube number.
This means
that a cube number is a number that is the product of three identical numbers.
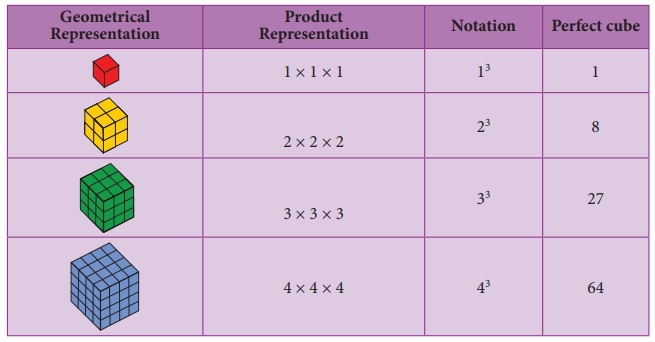
If n is a number, its cube is represented by n3.
Cube numbers
can be represented visually as 3D cubes comprising of single unit cubes. Cube numbers
are also called as perfect cubes. The perfect cubes of natural numbers are
1, 8, 27, 64, 125, 216, ... and so on.
Ramanujan Number - 1729 = 123+13 = 103+93
Once Professor
Hardy went to see Ramanujan when he was ill at Putney, riding in taxi cab number
1729 and said that the number seemed a dull one, and hoped it was not an unfavourable
omen. “No,” replied Ramanujan and he completed saying “It is a very interesting
number. Infact, it is the smallest number expressible as the sum of two cubes in
two different ways.” 4104, 13832, 20683 are a few more examples of Ramanujan-Hardy
numbers.
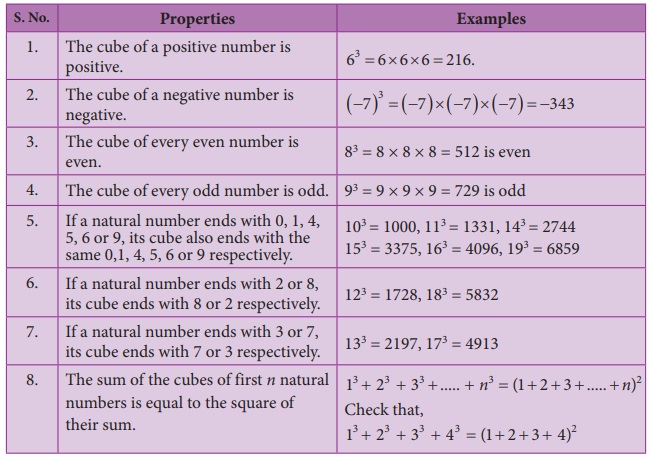
1. Properties
of cubes of numbers
Note
A perfect cube does not end with two zeroes.
The cube of a two digit number may have 4 or 5 or 6 digits in it.
Try these
Find the ones
digit in the cubes of each of the following numbers.
1. 12
2. 27
3. 38
4. 53
5. 71
6. 84
Solution:
(i) 12
12 ends with 2, so its cube ends with 8 i.e, ones digit in 123
is 8.
(2) 27
27 ends with 7, so its cube end with 3. i.e., ones digit in 273
is 3.
(3) 38
38 ends with 8, so its cube ends with 2 i.e, ones digit in 383
is 2.
(4) 53
53 ends with 3, so its cube ends with 7. i.e, ones digit in 533
is 7.
(5) 71
71 ends with 1, so its cube ends with 1. i.e, ones digit in 713
is 1
(6) 84
84 ends with 4, so its cube ends with 4. i.e, ones digit in 843
is 4.
2. Cube
root
The cube
root of a number is the value that when cubed gives the original number.
For example,
the cube root of 27 is 3 because when 3 is cubed we get 27.
Notation:
The cube
root of a number x is denoted as
3√x
(or) x1/3
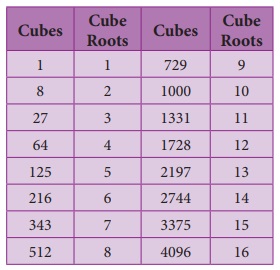
Here are
some more cubes and cube roots:
3√1 = 1 since 13 = 1, 3√8
= 2 since 23 = 8,
3√27 = 3 since 33 = 27, 3√64 = 4 since 43 = 64,
3√125 = 5 since 53 = 125 and so on.
Example 1.32
Is 400 a
perfect cube?
Solution:
By prime
factorisation, we have 400 = 2 × 2 × 2 × 2 × 5 × 5
There is
only one triplet. To make further triplets, we will need two more 2’s and one more
5.
Therefore,
400 is not a perfect cube.
Example 1.33
Find the
smallest number by which 675 must be multiplied to obtain a perfect cube.
Solution:

We find that,
675 = 3 × 3 × 3 × 5 × 5 …………….(1)
Grouping
the prime factors of 675 as triplets, we are left over with 5 × 5.
We need one
more 5 to make it a perfect cube.
To make 675
a perfect cube, multiply both sides of (1) by 5.
675×5=3×3×3×5×5×5
3375=3×3×3×5×5×5
Now, 3375
is a perfect cube. Thus, the smallest required number to multiply 675 such that
the new number perfect cube is 5.
Think
In this question, if the word ‘multiplied’ is replaced by the word
‘divided’, how will the solution vary?
3. Cube
root of a given number by Prime Factorisation
Step 1: Resolve
the given number into the product of prime factors.
Step 2: Make
triplet groups of same primes.
Step 3: Choosing
one from each triplet, find the product of primes to get the cube root.
Example 1.34
Find the
cube root of 27000.
Solution:
By prime
factorisation, we have 27000 = 2× 2 ×2× 3 × 3 × 3 × 5 × 5 ×5
∴ 3√27000 =
2×3×5
=30
Example 1.35
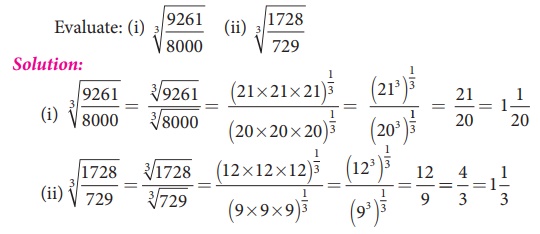
Related Topics