Definition, Formula, Solved Example Problems - The nth roots of unity | 12th Mathematics : UNIT 2 : Complex Numbers
Chapter: 12th Mathematics : UNIT 2 : Complex Numbers
The nth roots of unity
The nth roots of unity
The solutions of the equation zn = 1 , for positive values of integer n , are the n roots of the unity.
In polar form the equation zn = 1 can be written as
zn = cos (0 + 2kŽĆ) + i sin (0 + 2kŽĆ) = ei2kŽĆ , k = 0, 1, 2,ŌĆ”..
Using deMoivreŌĆÖs theorem, we find the nth roots of unity from the equation given below:
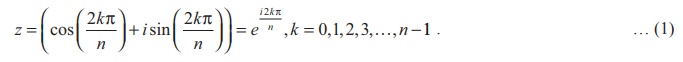
Given a positive integer n , a complex number z is called an n th root of unity if and only if zn = 1.
If we denote the complex number by Žē , then
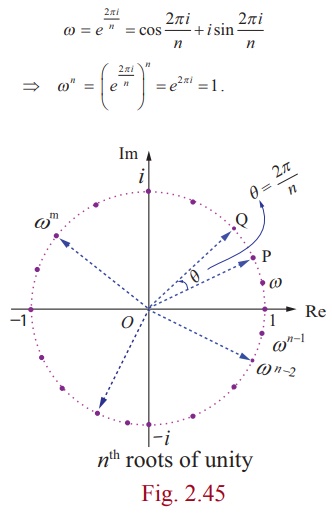
Therefore Žē is an nth root of unity. From equation (1), the complex numbers 1,Žē,Žē2 ,... ...,Žēn-1 are nth roots of unity. The complex numbers 1,Žē,Žē2 ,... ...,Žēn-1 are the points in the complex plane and are the vertices of a regular polygon of n sides inscribed in a unit circle as shown in Fig 2.45. Note that because the n th roots all have the same modulus 1, they will lie on a circle of radius 1 with centre at the origin. Furthermore, the n roots are equally spaced along the circle, because successive n th roots have arguments that differ by 2ŽĆ/n .
The nth roots of unity 1,Žē,Žē2 ,... ...,Žēn-1 are in geometric progression with common ratio Žē
Therefore 1+ Žē + Žē2 +ŌĆ” + Žēn-1 = 1- Žēn / 1- Žē = 0 since Žēn = 1 and Žē ŌēĀ 1 .
The sum of all the nth roots of unity is
1+ Žē + Žē2 +ŌĆ” + Žēn-1 = 0
The product of n, nth roots of unit is
1ŽēŽē2 ... ...Žēn-1 = Žē0+1+2+3+... ...+(n-1) = Žē[(n-1)n]/2
The product of all the nth roots of unity is
1ŽēŽē2 ... ...Žēn-1 = (-1)n-1

Note
(1) All the n roots of nth roots unity are in Geometrical Progression
(2) Sum of the n roots of nth roots unity is always equal to zero.
(3) Product of the n roots of nth roots unity is equal to (-1)n-1 .
(4) All the n roots of nth roots unity lie on the circumference of a circle whose centre is at the origin and radius equal to 1 and these roots divide the circle into n equal parts and form a polygon of n sides.
Example 2.32
Find the cube roots of unity.
Solution
We have to find 11/3 . Let z = 11/3 then z3 = 1.
In polar form, the equation z3 = 1 can be written as
z3 = cos(0 + 2kŽĆ) + i sin(0 + 2kŽĆ) = ei2kŽĆ , k = 0, 1, 2,...

Example 2.33
Find the fourth roots of unity.
Solution
We have to find 11/4. Let z =11/4 . Then z4 = 1 .
In polar form, the equation z4 = 1 can be written as
z4 = cos (0 + 2kŽĆ ) + i sin (0 + 2kŽĆ ) = ei2kŽĆ , k = 0, 1, 2,...

Note
(i) In this chapter the letter Žē is used for nth roots of unity. Therefore the value of Žē is depending on n as shown in following table.

(ii) The complex number zei╬Ė is a rotation of z by ╬Ė radians in the counter clockwise direction about the origin.
Example 2.34
Solve the equation z3 + 8i = 0 , where z Ōłł C.
Solution
Let z3 + 8i = 0 . Then, we get
z3 = -8i
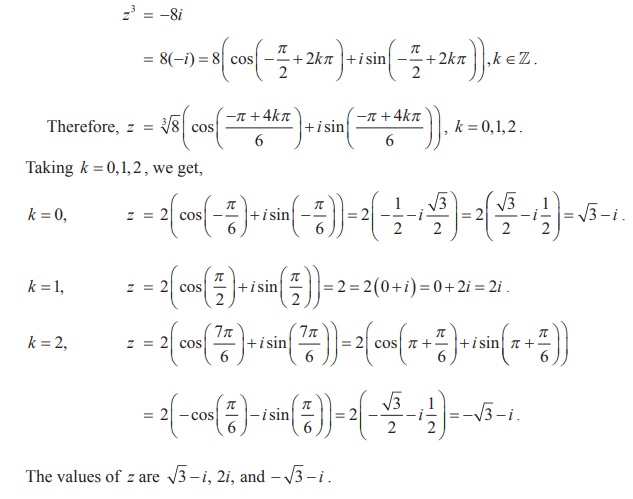
Example 2.35
Find all cube roots of ŌłÜ3 + i
Solution
We have to find (ŌłÜ3 + i)1/3. Let z3 = ŌłÜ3 + i = r (cos╬Ė + i sin╬Ė )
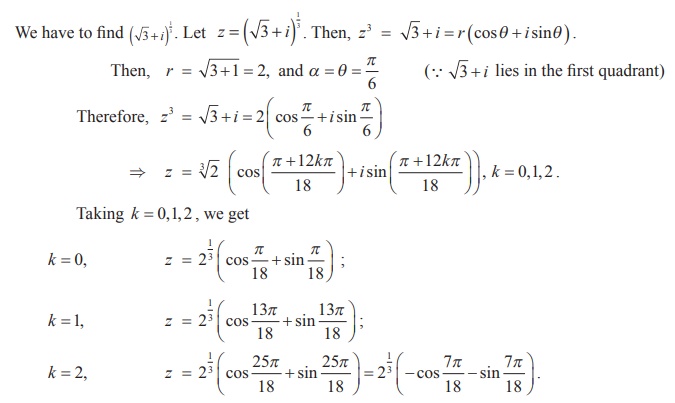
Example 2.36
Suppose z1 , z2, and z3 are the vertices of an equilateral triangle inscribed in the circle |z| = 2. If z1 = 1+ iŌłÜ3 , then find z2 and z3.
Solution
|z| = 2 represents the circle with centre (0, 0) and radius 2.
Let A, B, and C be the vertices of the given triangle. Since the vertices z1 , z2 , and z3 form an equilateral triangle inscribed in the circle |z| = 2 , the sides of this triangle AB, BC, and CA subtend 2ŽĆ/3 radians (120 degree) at the origin (circumcenter of the triangle).
(The complex number z ei╬Ė is a rotation of z by ╬Ė radians in the counter clockwise direction about the origin.)
Therefore, we can obtain z2 and z3 by the rotation of z1 by 2ŽĆ/3 and 4 ŽĆ/3 respectively.
Given that
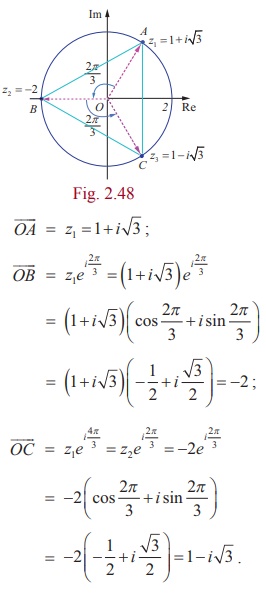
Therefore, z2 = -2, and z3 = 1- iŌłÜ3.
Related Topics