The general equation of a Conic

The general equation of a Conic

Let S ( x₁ , y₁ ) be the focus, l the directrix, and e be the eccentricity. Let P ( x, y ) be the moving point.

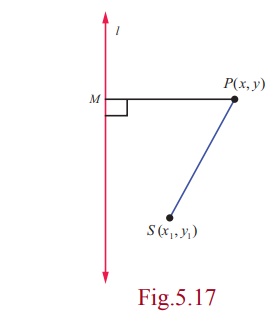
By the definition of conic, we have

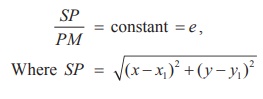
and PM = perpendicular distance from P(x, y) to the line lx + my + n = 0

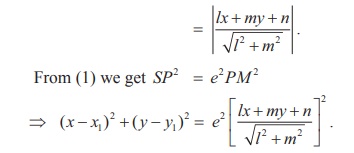
On simplification the above equation takes the form of general second-degree equation

Ax² + Bxy + Cy² + Dx + Ey + F = 0 , where

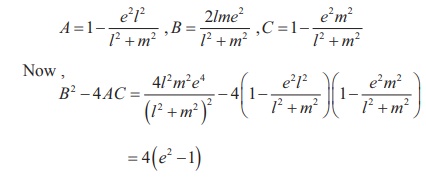
yielding the following cases:

(i) B² - 4 AC = 0 Û e = 1 Û the conic is a parabola,

(ii) B² - 4 AC < 0 Û 0 < e <1 Û the conic is an ellipse,

(iii) B² - 4 AC > 0 Û e >1 Û the conic is a hyperbola.