Condition for the line y = mx + c to be a tangent to the circle and finding the point of contact

Condition for the line y = mx + c to be a tangent to the circle x² + y² = a² and finding the point of contact

Let the line y = mx + c touch the circle x² + y² = a² . The centre and radius of the circle x² + y² = a² are (0, 0) and a respectively.

(i) Condition for a line to be tangent

Then the perpendicular distance of the line y − mx − c = 0 from (0, 0) is

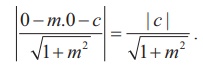
This must be equal to radius .Therefore 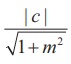 = a or c² = a² (1+ m²) .

Thus the condition for the line y = mx + c to be a tangent to the circle x² + y² = a² is c² = a² (1 + m²).

(ii) Point of contact

Let (x₁ , y₁ ) be the the point of contact of y = mx + c with the circle x² + y² = a²,

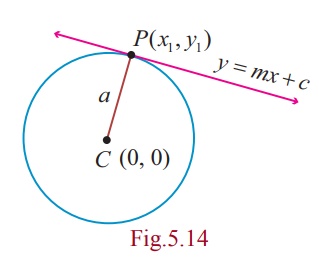
Then  y₁ =  mx₁ + c       ……….(1)

Equation of tangent at (x₁ , y₁ ) is xx₁ + yy₁ = a² .

yy₁  =  -xx₁ + a²       ... (2)

Equations (1) and (2) represent the same line and hence the coefficients are proportional.

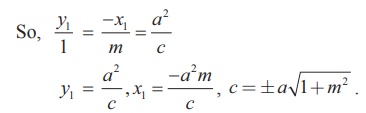
Then the points of contact is either

Note 

The equation of tangent at P to a circle is y = mx ± a √[1 +m²]

Theorem 5.4

From any point outside the circle x² + y² = a² two tangents can be drawn.

Proof

Let P(x₁ , y₁ ) be a point outside the circle. The equation of the tangent is

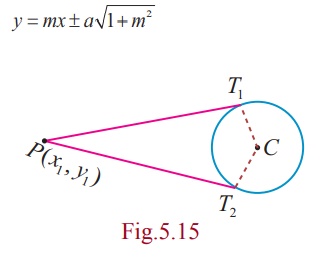
It passes through (x₁, y₁) . Therefore

Squaring both sides, we get

( y₁ – mx₁)² = a² (1+ m² )

y₁² + m² x₁² - 2mx₁y₁ - a² - a²m² = 0

m² (x₁² - a² ) - 2mx₁y₁ + ( y₁² - a² ) = 0 .

This quadratic equation in m gives two values for m .

These values give two tangents to the circle x² + y² = a².

Note

(1)  If (x₁, y₁ ) is a point outside the circle, then both the tangents are real.

(2)  If (x₁, y₁ ) is a point inside the circle, then both the tangents are imaginary.

(3)  If (x₁, y₁ ) is a point on the circle, then both the tangents coincide.

Example 5.11

Find the equations of the tangent and normal to the circle x² + y² = 25 at P(−3, 4) .

Solution

Equation of tangent to the circle at P(x₁ , y₁ ) is xx₁ + yy₁ = a² 

That is, x(-3) + y(4) = 25

-3x + 4 y = 25

Equation of normal is xy₁ - yx₁ = 0

That is, 4x + 3y = 0 .

Example 5.12

If y = 4x + c is a tangent to the circle x² + y² = 9 , find c.

Solution

The condition for the line y = mx + c to be a tangent to the circle x² + y² = a² is c² = a² (1+ m²).

Then, c = ± √[9(1+16)]

c = ±3 √17.

Example 5.13

A road bridge over an irrigation canal have two semi circular vents each with a span of 20m and the supporting pillars of width 2m . Use Fig.5.16 to write the equations that represent the semi-verticular vents.

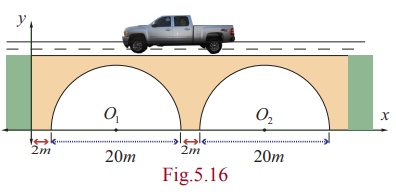
Solution

Let  O₁ O₂  be  the  centres  of  the two semi circular vents.

First vent with centre O₁ (12, 0) and radius r = 10 yields equation to first semicircle as

(x -12)² + ( y - 0)² = 10²

Þ x² + y² - 24x + 44 = 0 , y > 0 .

Second vent with centre O₂ (34, 0) and radius r = 10 yields equation to second vent as

(x - 34)² + y² = 10²

Þ x² + y² - 68x +1056 = 0 , y > 0 .