Equations of tangent and normal at a point P on a given circle

Equations of tangent and normal at a point P on a given circle

Tangent of a circle is a line which touches the circle at only one point and normal is a line perpendicular to the tangent and passing through the point of contact.

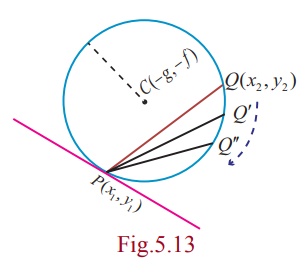
Let P(x₁ , y₁ ) and Q(x₂ , y₂ ) be two points on the circle x² + y² + 2gx + 2 fy + c = 0 .

Therefore,

x₁² + y₁² + 2gx₁ + 2 fy₁ + c = 0 ... (1)

and x₂² + y₂² + 2gx₂ + 2fy₂+ c = 0  ……..(2)

(2) - (1) gives

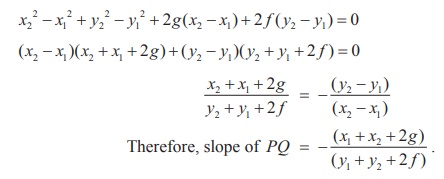
Therefore, slope of PQ = - (x₁ + x₂ + 2g) / ( y₁  + y₂ + 2f )

When Q → P, the chord PQ becomes tangent at P

 Slope  of tangent is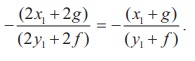 

Hence, the equation of tangent is  y – y₁ = 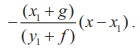 Simplifying

 yy₁ + fy – y₁² - fy₁ + xx₁ - x₁² + gx - gx₁ = 0

 xx₁  + yy₁  + gx + fy - (x₁²  + y₁²  + gx₁  + fy₁ ) = 0 ...(1)

Since (x₁ , y₁ ) is a point on the circle, we have x₁² + y₁² + 2gx₁ + 2 fy₁ + c = 0

Therefore, -(x₁² + y₁² + gx + fy ) = gx₁ + fy₁ + c (2)

Hence, substituting (2) in (1), we get the equation of tangent at (x₁ , y₁ ) as

xx₁ + yy₁ + g(x + x₁ ) + f ( y + y₁ ) + c = 0 .

Hence, the equation of normal is

( y – y₁ ) = [ ( y₁ + f ) / ( x₁  + g ) ] ( x – x₁ )

Þ ( y - y₁ )( x₁ + g ) = ( y₁  + f )( x - x₁ )

Þ x₁ ( y - y₁ ) + g ( y - y₁ ) = y₁ ( x - x₁ ) + f ( x - x₁ )

Þ yx₁ - xy₁ + g ( y - y₁ ) - f ( x - x₁ ) = 0 .

Remark

(1) The equation of tangent at ( x₁ , y₁ ) to the circle x²+y² = a² is xx₁ + yy₁ = a².

(2) The equation of normal at ( x₁ , y₁ ) to the circle x²+y² = a² is xy₁ - yx₁ = 0 .

(3) The normal passes through the centre of the circle.