Choose the correct Answer

Choose the correct or the most suitable answer from the given four alternatives :

1. The equation of the circle passing through (1, 5) and (4,1) and touching y -axis is x2 + y2 − 5x − 6 y + 9 + λ (4x + 3y −19) = 0 where λ is equal to

(1) 0, - 40/9

(2) 0

(3) 40/9

(4) -40/9

2. The eccentricity of the hyperbola whose latus rectum is 8 and conjugate axis is equal to half the distance between the foci is

(1) 4/3

(2) 4/√3

(3) 2√3

(4) 3/2

3. The circle x2 + y2 = 4x + 8 y + 5 intersects the line 3x − 4 y = m at two distinct points if

(1) 15 < m < 65

(2) 35 < m < 85

(3) -85 < m < -35

(4) -35 < m < 15

4. The length of the diameter of the circle which touches the x -axis at the point (1,0) and passes through the point (2, 3) .

(1) 6/5

(2) 5/3

(3) 10/3

(4) 3/5

5. The radius of the circle 3x2 + by2 + 4bx − 6by + b2 = 0 is

(1) 1

(2) 3

(3) √10

(3) √11

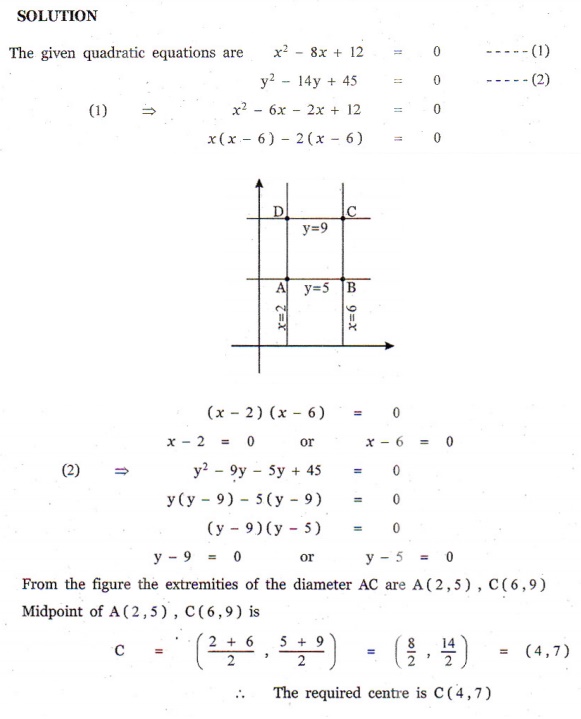
6. The centre of the circle inscribed in a square formed by the lines x2 − 8x −12 = 0 and  y2 −14 y + 45 = 0 is

(1) (4, 7)

(2) (7, 4)

(3) (9, 4)

(4) (4, 9)

7. The equation of the normal to the circle x2 + y2 − 2x − 2 y +1 = 0 which is parallel to the line 2x + 4 y = 3 is

(1) x + 2 y = 3

(2) x + 2 y + 3 = 0

(3) 2 x + 4 y + 3 = 0

(4) x - 2 y + 3 = 0

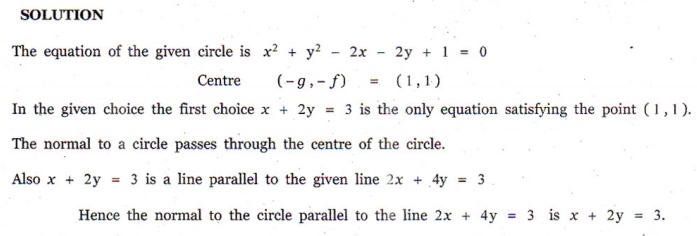
8. If P(x, y) be any point on 16x2 + 25 y2 = 400 with foci F1 (3, 0) and F2 (−3, 0) then PF1 + PF2 is

(1) 8

(2) 6

(3) 10

(4) 12

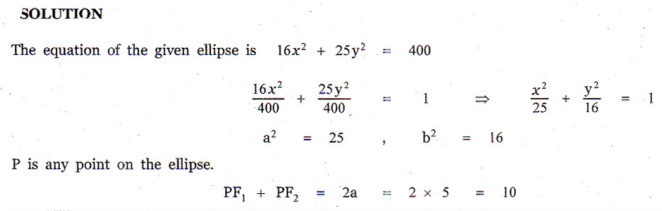
9. The radius of the circle passing through the point (6, 2) two of whose diameter are x + y = 6 and x + 2 y = 4 is

(1) 10

(2) 2√5

(3) 6

(4) 4

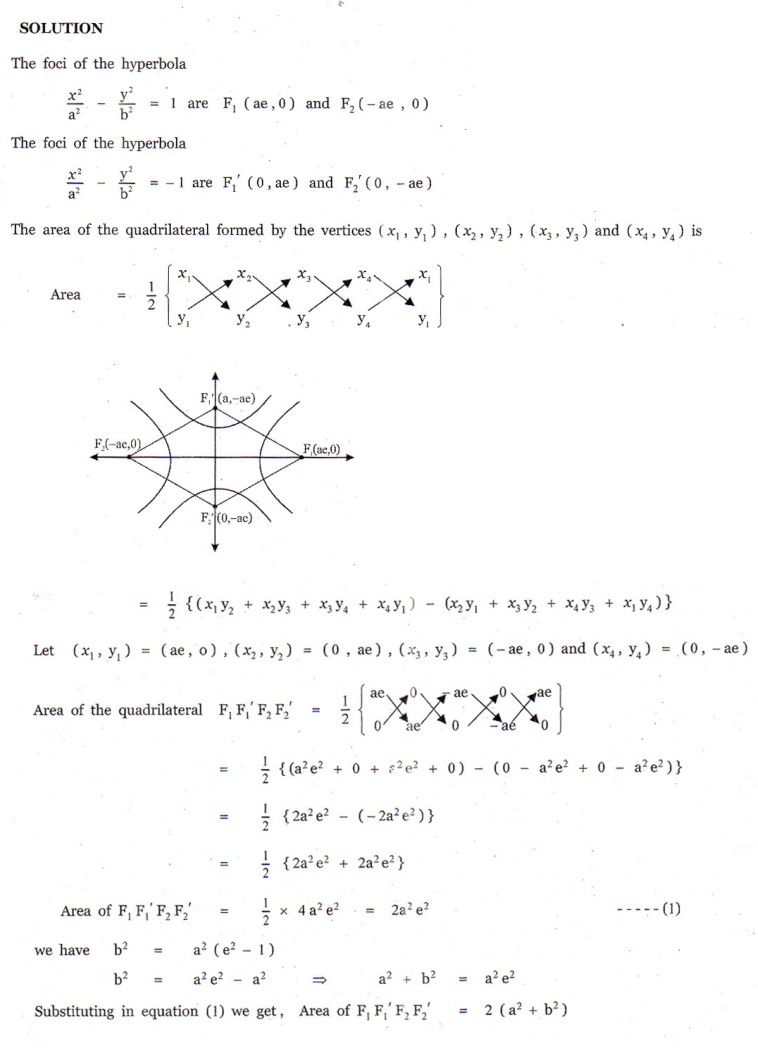
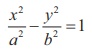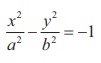10. The area of quadrilateral formed with foci of the hyperbolas  and  is

(1) 4(a2 + b2 )

(2) 2(a2 + b2 )

(3) a2 + b2

(4) 1/2 (a2 + b2 )

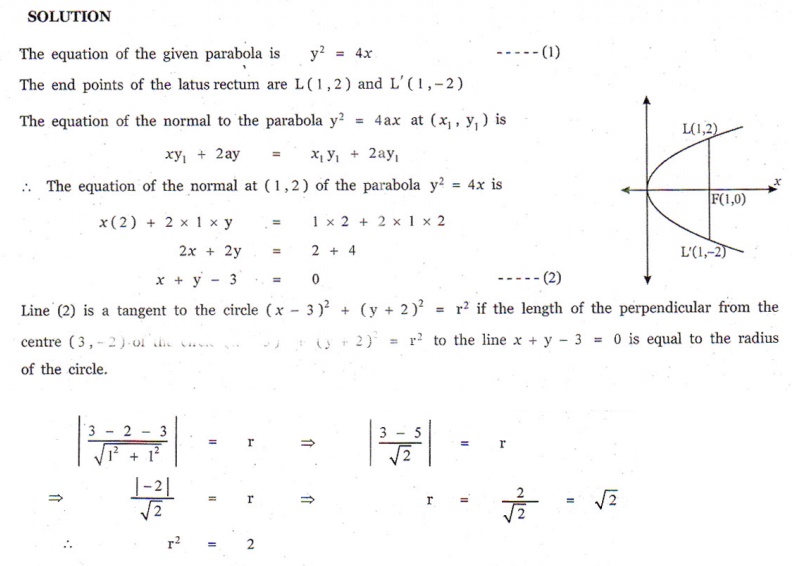
11. If the normals of the parabola y2 = 4x drawn at the end points of its latus rectum are tangents to the circle (x − 3)2 + ( y + 2)2 = r 2 , then the value of r 2 is

(1) 2

(2) 3

(3) 1

(4) 4

12. If x + y = k is a normal to the parabola y2 = 12x , then the value of k is

(1) 3

(2) -1

(3) 1

(4) 9

13. The ellipse E1 : 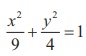 is inscribed in a rectangle R whose sides are parallel to the coordinate axes. Another ellipse E2 passing through the point (0, 4) circumscribes the rectangle R . The eccentricity of the ellipse is

(1) √2/2

(2) √3/2

(3) 1/2

(4) 3/4

14. Tangents are drawn to the hyperbola 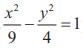 parallel to the straight line 2x − y = 1. One ofthe points of contact of tangents on the hyperbola is

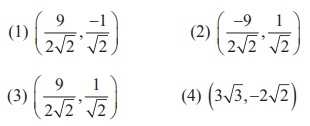
Ans: (3)

15. The equation of the circle passing through the foci of the ellipse 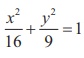 having centre at (0,3) is

(1) x2 + y2 - 6 y - 7 = 0

(2) x2 + y2 - 6 y + 7 = 0

(3) x2 + y2 - 6 y - 5 = 0

(4) x2 + y2 - 6 y + 5 = 0

16. Let C be the circle with centre at (1,1) and radius = 1 . If T is the circle centered at (0, y) passing through the origin and touching the circle Cexternally, then the radius of T is equal to

(1)  √3/√2

(2) √3/2

(3) 1/2

(4) 1/4

17. Consider an ellipse whose centre is of the origin and its major axis is along x-axis. If its eccentrcity is 3/5 and the distance between its foci is 6, then the area of the quadrilateral inscribed in the ellipse with diagonals as major and minor axis of the ellipse is

(1) 8

(2) 32

(3) 80

(4) 40

18. Area of the greatest rectangle inscribed in the ellipse 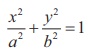 is

(1) 2ab

(2) ab

(3) √ab

 (4) a/b

19. An ellipse has OB as semi minor axes, F and F ′ its foci and the angle FBF ′ is a right angle. Then the eccentricity of the ellipse is

(1) 1/√2

(2) 1/2

(3) 1/4

(4) 1/√3

20. The eccentricity of the ellipse (x - 3)2 + ( y - 4)2 = y2/9 is

(1)  √3 / 2

(2) 1 / 3

 (3) 1 / 3√2

(4) 1 / √3

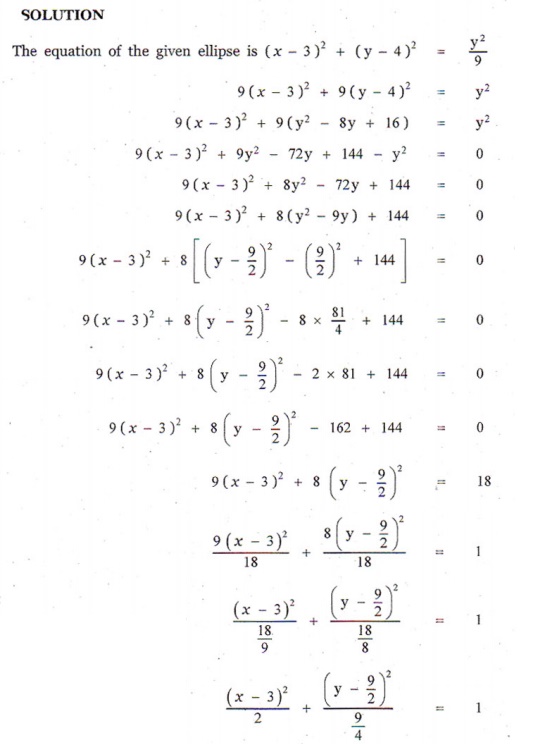
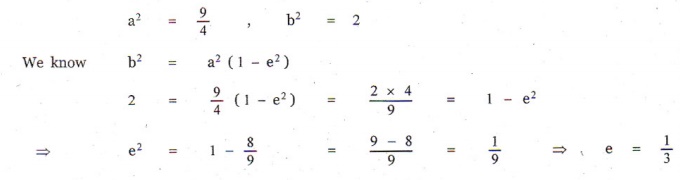
21. If the two tangents drawn from a point P to the parabola y2 = 4x are at right angles then the locus of P is

(1) 2x +1 = 0

(2) x = -1

(3) 2x -1 = 0

(4) x = 1

22. The circle passing through (1, −2) and touching the axis of x at (3, 0) passing through the point

(1) (-5, 2)

(2) (2, -5)

(3) (5, -2)

(4) (-2, 5)

23. The locus of a point whose distance from (−2, 0) is 2/3 times its distance from the line x=-9/2 is

(1) a parabola

(2) a hyperbola

(3) an ellipse

(4) a circle

24. The values of m for which the line y = mx + 2√5  touches the hyperbola 16x2 − 9 y2 = 144 are the roots of x2 − (a + b)x − 4 = 0 , then the value of (a + b) is

(1) 2

(2) 4

(3) 0

(4) -2

25. If the coordinates at one end of a diameter of the circle x2 + y2 − 8x − 4 y + c = 0 are (11, 2) , the coordinates of the other end are

(1) (-5, 2)

(2) (2, -5)

(3) (5, -2)

(4) (-2, 5)

Choose the correct or the most suitable answer from the given four alternatives :

1. The equation of the circle passing through (1, 5) and (4,1) and touching y -axis is x2 + y2 − 5x − 6 y + 9 + λ (4x + 3y −19) = 0 where λ is equal to

(1) 0, - 40/9

(2) 0

(3) 40/9

(4) -40/9

2. The eccentricity of the hyperbola whose latus rectum is 8 and conjugate axis is equal to half the distance between the foci is

(1) 4/3

(2) 4/√3

(3) 2√3

(4) 3/2

3. The circle x2 + y2 = 4x + 8 y + 5 intersects the line 3x − 4 y = m at two distinct points if

(1) 15 < m < 65

(2) 35 < m < 85

(3) -85 < m < -35

(4) -35 < m < 15

4. The length of the diameter of the circle which touches the x -axis at the point (1,0) and passes through the point (2, 3) .

(1) 6/5

(2) 5/3

(3) 10/3

(4) 3/5

5. The radius of the circle 3x2 + by2 + 4bx − 6by + b2 = 0 is

(1) 1

(2) 3

(3) √10

(3) √11

6. The centre of the circle inscribed in a square formed by the lines x2 − 8x −12 = 0 and  y2 −14 y + 45 = 0 is

(1) (4, 7)

(2) (7, 4)

(3) (9, 4)

(4) (4, 9)

7. The equation of the normal to the circle x2 + y2 − 2x − 2 y +1 = 0 which is parallel to the line 2x + 4 y = 3 is

(1) x + 2 y = 3

(2) x + 2 y + 3 = 0

(3) 2 x + 4 y + 3 = 0

(4) x - 2 y + 3 = 0

8. If P(x, y) be any point on 16x2 + 25 y2 = 400 with foci F1 (3, 0) and F2 (−3, 0) then PF1 + PF2 is

(1) 8

(2) 6

(3) 10

(4) 12

9. The radius of the circle passing through the point (6, 2) two of whose diameter are x + y = 6 and x + 2 y = 4 is

(1) 10

(2) 2√5

(3) 6

(4) 4

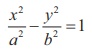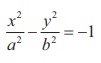10. The area of quadrilateral formed with foci of the hyperbolas  and  is

(1) 4(a2 + b2 )

(2) 2(a2 + b2 )

(3) a2 + b2

(4) 1/2 (a2 + b2 )

11. If the normals of the parabola y2 = 4x drawn at the end points of its latus rectum are tangents to the circle (x − 3)2 + ( y + 2)2 = r 2 , then the value of r 2 is

(1) 2

(2) 3

(3) 1

(4) 4

12. If x + y = k is a normal to the parabola y2 = 12x , then the value of k is

(1) 3

(2) -1

(3) 1

(4) 9

13. The ellipse E1 : 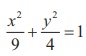 is inscribed in a rectangle R whose sides are parallel to the coordinate axes. Another ellipse E2 passing through the point (0, 4) circumscribes the rectangle R . The eccentricity of the ellipse is

(1) √2/2

(2) √3/2

(3) 1/2

(4) 3/4

14. Tangents are drawn to the hyperbola 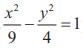 parallel to the straight line 2x − y = 1. One ofthe points of contact of tangents on the hyperbola is

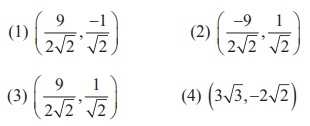
Ans: (3)

15. The equation of the circle passing through the foci of the ellipse 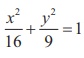 having centre at (0,3) is

(1) x2 + y2 - 6 y - 7 = 0

(2) x2 + y2 - 6 y + 7 = 0

(3) x2 + y2 - 6 y - 5 = 0

(4) x2 + y2 - 6 y + 5 = 0

16. Let C be the circle with centre at (1,1) and radius = 1 . If T is the circle centered at (0, y) passing through the origin and touching the circle Cexternally, then the radius of T is equal to

(1)  √3/√2

(2) √3/2

(3) 1/2

(4) 1/4

17. Consider an ellipse whose centre is of the origin and its major axis is along x-axis. If its eccentrcity is 3/5 and the distance between its foci is 6, then the area of the quadrilateral inscribed in the ellipse with diagonals as major and minor axis of the ellipse is

(1) 8

(2) 32

(3) 80

(4) 40

18. Area of the greatest rectangle inscribed in the ellipse 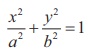 is

(1) 2ab

(2) ab

(3) √ab

 (4) a/b

19. An ellipse has OB as semi minor axes, F and F ′ its foci and the angle FBF ′ is a right angle. Then the eccentricity of the ellipse is

(1) 1/√2

(2) 1/2

(3) 1/4

(4) 1/√3

20. The eccentricity of the ellipse (x - 3)2 + ( y - 4)2 = y2/9 is

(1)  √3 / 2

(2) 1 / 3

 (3) 1 / 3√2

(4) 1 / √3

21. If the two tangents drawn from a point P to the parabola y2 = 4x are at right angles then the locus of P is

(1) 2x +1 = 0

(2) x = -1

(3) 2x -1 = 0

(4) x = 1

22. The circle passing through (1, −2) and touching the axis of x at (3, 0) passing through the point

(1) (-5, 2)

(2) (2, -5)

(3) (5, -2)

(4) (-2, 5)

23. The locus of a point whose distance from (−2, 0) is 2/3 times its distance from the line x=-9/2 is

(1) a parabola

(2) a hyperbola

(3) an ellipse

(4) a circle

24. The values of m for which the line y = mx + 2√5  touches the hyperbola 16x2 − 9 y2 = 144 are the roots of x2 − (a + b)x − 4 = 0 , then the value of (a + b) is

(1) 2

(2) 4

(3) 0

(4) -2

25. If the coordinates at one end of a diameter of the circle x2 + y2 − 8x − 4 y + c = 0 are (11, 2) , the coordinates of the other end are

(1) (-5, 2)

(2) (2, -5)

(3) (5, -2)

(4) (-2, 5)