Exercise 5.2: Conics

EXERCISE 5.2

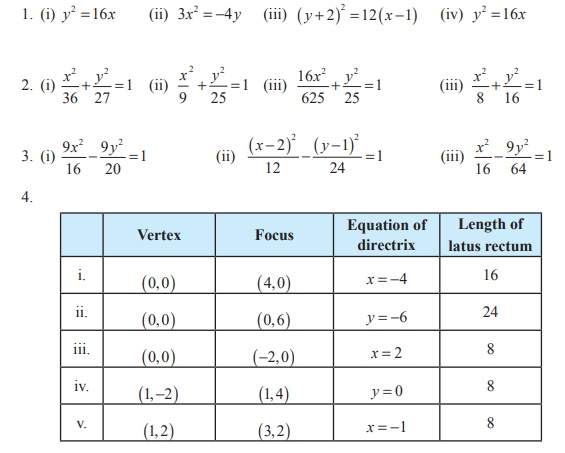
1. Find the equation of the parabola in each of the cases given below:

(i) focus (4, 0) and directrix x = -4 .

(ii) passes through (2, -3) and symmetric about y -axis.

(iii) vertex (1, -2) and focus (4, -2) .

(iv) end points of latus rectum (4, -8) and (4,8) .

2. Find the equation of the ellipse in each of the cases given below:

(i) foci ( ±3, 0), e = 1/2.

(ii) foci (0, ±4) and end points of major axis are(0,±5) .

(iii) length of latus rectum 8, eccentricity = 3/5 and major axis on x -axis.

(iv) length of latus rectum 4 , distance between foci 4√2 and major axis as y - axis.

3. Find the equation of the hyperbola in each of the cases given below:

(i) foci ( ±2, 0) , eccentricity = 3/2 .

(ii) Centre (2,1) , one of the foci (8,1) and corresponding directrix x = 4 .

(iii) passing through(5, -2) and length of the transverse axis along x axis and of length 8 units.

4. Find the vertex, focus, equation of directrix and length of the latus rectum of the following:

(i) y2 = 16x

(ii) x2 = 24 y

(iii) y2 = -8x

(iv) x2 − 2x + 8 y +17 = 0

(v) y2 - 4 y - 8x +12 = 0

5. Identify the type of conic and find centre, foci, vertices, and directrices of each of the following:

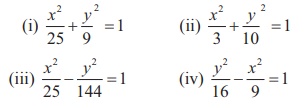
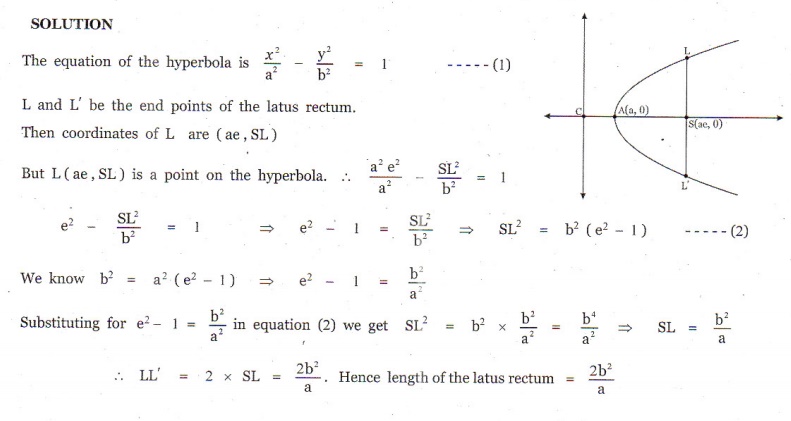
6. Prove that the length of the latus rectum of the hyperbola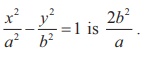 

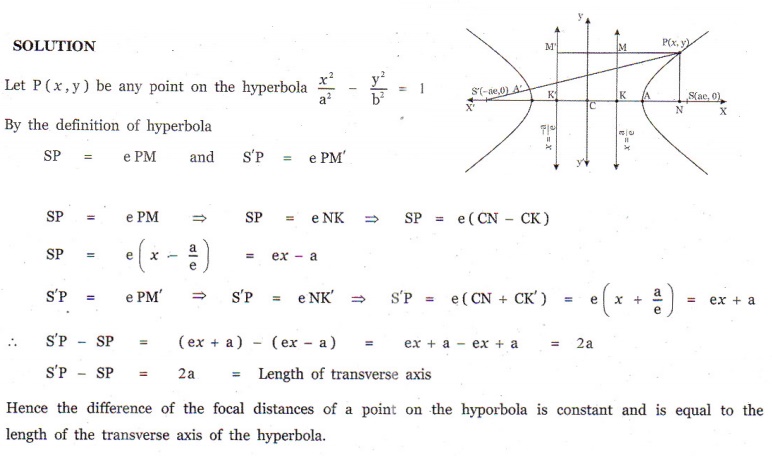
7. Show that the absolute value of difference of the focal distances of any point P on the hyperbola is the length of its transverse axis.

8. Identify the type of conic and find centre, foci, vertices, and directrices of each of the following :

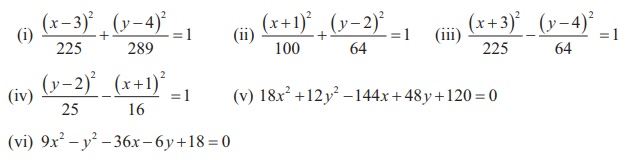
Answers: