Chapter: 12th Mathematics : UNIT 5 : Two Dimensional Analytical Geometry II
Solved Example Problems on Real life Applications of Conics
Example 5.30
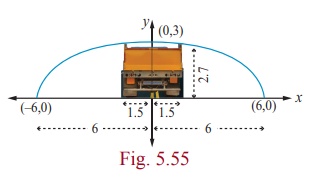
A semielliptical archway over a one-way road has a height of 3m and a width of 12m . The truck has a width of 3m and a height of 2.7m . Will the truck clear the opening of the archway? (Fig. 5.6)
Solution
Since the truck’s width is 3m , to determine the clearance, we must find the height of the archway 1.5m from the centre. If this height is 2.7m or less the truck will not clear the archway.
From the diagram a = 6 and b = 3 yielding the equation of elipse as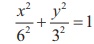 
.
The edge of the 3m wide truck corresponds to x = 1.5m from centre We will find the height of the archway 1.5m from the centre by substituting x = 1.5 and solving for y
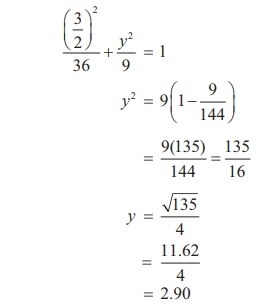
Thus the height of arch way 1.5m from the centre is approximately 2.90m . Since the truck’s height is 2.7m , the truck will clear the archway.
Example 5.31
The maximum and minimum distances of the Earth from the Sun respectively are 152 ×106 km and 94.5×106 km. The Sun is at one focus of the elliptical orbit. Find the distance from the Sun to the other focus.
Solution
AS = 94.5×106 km, SA ' = 152 ×106 km
a + c = 152 ×106
a − c = 94.5×106
Subtracting 2c = 57.5×106 = 575×105 km
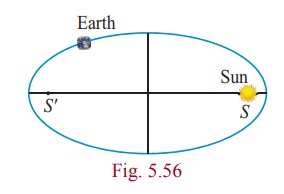
Distance of the Sun from the other focus is SS′ = 575×105 km.
Example 5.32
A concrete bridge is designed as a parabolic arch. The road over bridge is 40m long and the maximum height of the arch is 15m . Write the equation of the parabolic arch.
Solution
From the graph the vertex is at (0, 0) and the parabola is open down
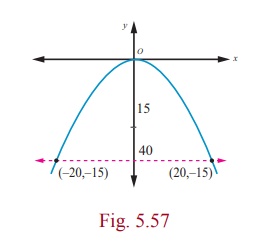
Equation of the parabola is x2 = −4ay
(−20, −15) and (20, −15) lie on the parabola
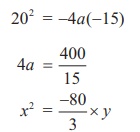
Therefore equation is 3x2=-80y
Example 5.33
The parabolic communication antenna has a focus at 2m distance from the vertex of the antenna. Find the width of the antenna 3m from the vertex.
Solution
Let the parabola be y2 = 4ax .
Since focus is 2m from the vertex a = 2
Equation of the parabola is y2 = 8x
Let P be a point on the parabola whose x -coordinate is 3m from the vertex P (3, y)
y2 = 8´ 3
y = √(8x3)
= 2√6
The width of the antenna 3m from the vertex is 4√6 m.
Example 5.34
The equation y = (1/32) x2 models cross sections of parabolic mirrors that are used for solar energy. There is a heating tube located at the focus of each parabola; how high is this tube located above the vertex of the parabola?
Solution
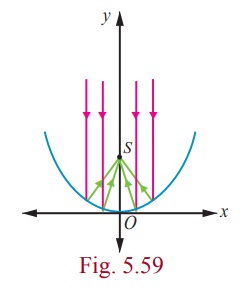
Equation of the parabola is
y = (1/32) x2
That is x2 = 32y ; the vertex is (0, 0)
= 4(8) y
⇒ a = 8
So the heating tube needs to be placed at focus (0, a) . Hence the heating tube needs to be placed 8 units above the vertex of the parabola.
Example 5.35
A search light has a parabolic reflector (has a cross section that forms a ‘bowl’). The parabolic bowl is 40 cm wide from rim to rim and 30 cm deep. The bulb is located at the focus .
(1) What is the equation of the parabola used for reflector?
(2) How far from the vertex is the bulb to be placed so that the maximum distance covered?
Solution
Let the vertex be (0, 0) .
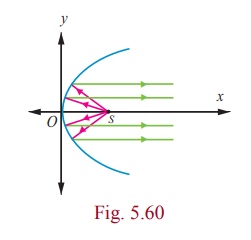
The equation of the parabola is
y2 = 4ax
(1) Since the diameter is 40 cm and the depth is 30 cm , the point (30,20) lies on the parabola.
202 = 4a ´ 30
4a = 400/30 = 40/3 .
Equation is y2 = 40/3 x.
(2) The bulb is at focus (0, a) . Hence the bulb is at a distance of 10/3 cm from the vertex.
Example 5.36
An equation of the elliptical part of an optical lens system is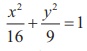 
.
The parabolic part of the system has a focus in common with the right focus of the ellipse .The vertex of the parabola is at the origin and the parabola opens to the right. Determine the equation of the parabola.
Solution
In the given ellipse a2 = 16 , b2 = 9
then c2 = a2 - b2
c2 = 16 – 9
= 7
c = ± √7
Therefore the foci are F ( √7, 0), F ¢(-√7, 0) . The focus of the parabola is (√7, 0) ⇒ a =√7 Equation of the parabola is y2 = 4√7x .
Example 5.37
A room 34m long is constructed to be a whispering gallery. The room has an elliptical ceiling, as shown in Fig. 5.64. If the maximum height of the ceiling is 8m , determine where the foci are located.
Solution
The length a of the semi major axis of the elliptical ceiling is 17m . The height b of the semi minor axis is 8m . Thus
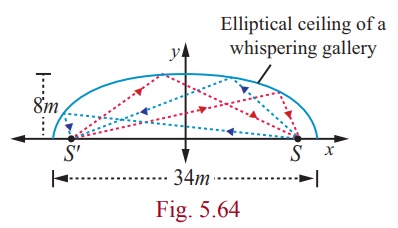
c2 = a2 - b2 = 172 - 82
then c = √[289 – 64] = √225
= 15
For the elliptical ceiling the foci are located on either side about 15m from the centre, along its major axis.
A non-invasive medical miracle
In a lithotripter, a high-frequency sound wave is emitted from a source that is located at one of the foci of the ellipse. The patient is placed so that the kidney stone is located at the other focus of the ellipse.
Example 5.38
If the equation of the ellipse is 
( x and y are measured in centimeters) where to the nearest centimeter, should the patient’s kidney stone be placed so that the reflected sound hits the kidney stone?
Solution
The equation of the ellipse is .
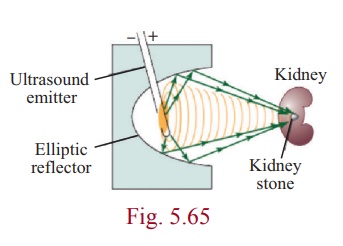
The origin of the sound wave and the kidney stone of patient should be at the foci in order to crush the stones.
a2 = 484 and b2 = 64
c2 = a2 - b2
= 484 -64
= 420
c ≈ 20.5
Therefore the patient’s kidney stone should be placed 20.5cm from the centre of the ellipse.
Example 5.39
Two coast guard stations are located 600 km apart at points A(0, 0) and B(0, 600) . A distress signal from a ship at P is received at slightly different times by two stations. It is determined that the ship is 200 km farther from station A than it is from station B . Determine the equation of hyperbola that passes through the location of the ship.
Solution
Since the centre is located at (0, 300) , midway between the two foci,which are the coast guard stations, the equation is
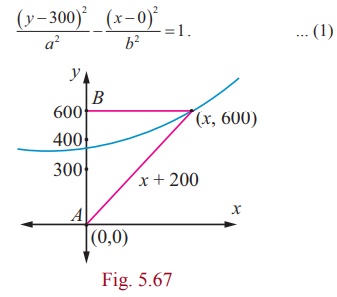
To determine the values of a and b , select two points known to be on the hyperbola and substitute each point in the above equation.
The point (0, 400) lies on the hyperbola, since it is 200 km further from Station A than from station B .
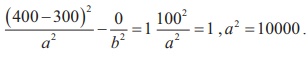
There is also a point (x, 600) on the hyperbola such that 6002 + x2 = ( x + 200)2.
360000 + x2 = x2 + 400x + 40000
x = 800
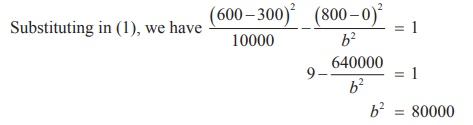
Thus the required equation of the hyperbola is
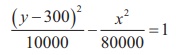
The ship lies somewhere on this hyperbola. The exact location can be determined using data from a third station.
Example 5.40
Certain telescopes contain both parabolic mirror and a hyperbolic mirror. In the telescope shown in figure 5.68 the parabola and hyperbola share focus F1 which is 14m above the vertex of the parabola. The hyperbola’s second focus F2 is 2m above the parabola’s vertex. The vertex of the hyperbolic mirror is 1m below F1. Position a coordinate system with the origin at the centre of the hyperbola and with the foci on the y -axis. Then find the equation of the hyperbola.
Solution
Let V1 be the vertex of the parabola and V2 be the vertex of the hyperbola.
= 14 - 2 = 12m, 2c = 12, c = 6
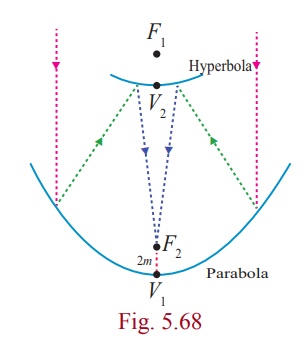
The distance of centre to the vertex of the hyperbola is a = 6 −1 = 5
b2 = c2 - a2
= 36 - 25 = 11.
Therefore the equation of the hyperbola is y2/25 - x2/11 = 1
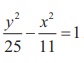
Related Topics