Chapter: 12th Mathematics : UNIT 5 : Two Dimensional Analytical Geometry II
Real life Applications of Conics
Real
life Applications of Conics
1. Parabola
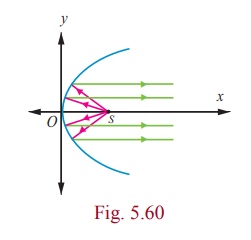
The interesting applications of Parabola involve their use as
reflectors and receivers of light or radio waves. For instance, cross sections
of car headlights, flashlights are parabolas wherein the gadgets are formed by
the paraboloid of revolution about its axis. The bulb in the headlights, flash
lights is located at the focus and light from that point is reflected outward
parallel to the axis of symmetry (Fig. 5.60) while Satellite dishes and field
microphones used at sporting events, incoming radio waves or sound waves
parallel to the axis that are reflected into the focus intensifying the same
(Fig. 5.59). Similarly, in solar cooking, a parabolic mirror is mounted on a
rack with a cooking pot hung in the focal area (Fig. 5.1). Incoming Sun rays
parallel to the axis are reflected into the focus producing a
temperature high enough for cooking.
Parabolic arches are the best stable structures also considered
for their beauty to name a few, the arches on the bridge of river in Godavari, Andhra Pradesh,
India, the Eiffel tower in Paris, France.

2. Ellipse
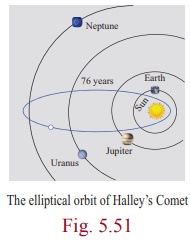
According to Johannes Kepler, all planets in the solar system
revolve around Sun in elliptic orbits with Sun at one of the foci. Some comets
have elliptic orbits with Sun at one of the foci as well. E.g. Halley’s Comet
that is visible once every 75 years with e » 0.97 in elliptic orbit
(Fig. 5.51). Our satellite moon travels around the Earth in an elliptical orbit
with earth at one of its foci. Satellites of other planets also revolve around
their planets in elliptical orbits as well.
Elliptic arches are often built for its beauty and stability. Steam boilers are believed to have greatest strength when heads are made elliptical with major and minor axes in the ratio 2:1.
In Bohr-Sommerfeld theory of the atom electron orbit can be
circular or elliptical. Gears are sometimes (for particular need) made
elliptical in shape. (Fig. 5.52)
The shape of our mother Earth is an oblate spheroid i.e., the
solid of revolution of an ellipse about its minor axis, bulged along equatorial
region and flat along the polar region.
The property of ellipse, any ray of light or sound released from
a focus of the ellipse on touching the ellipse gets reflected to reach the
other focus (Fig. 5.62), which could be proved using concepts of incident rays and reflected rays in Physics.
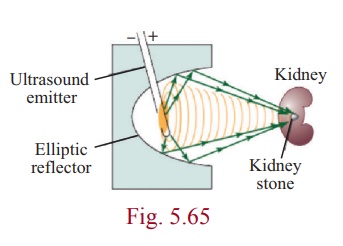
An exciting medical application of an ellipsoidal reflectors is
a device called a Lithotripter (Fig. 5.4 and 5.63) that uses electromagnetic
technology or ultrasound to generate a shock wave to pulverize kidney stones.
The wave originates at one focus of the cross-sectional ellipse and is
reflected to the kidney stone, which is positioned at the other focus. Recovery
time following the use of this technique is much shorter than the conventional
surgery, non-invasive and the mortality rate is lower.
3. Hyperbola
Some Comets travel in hyperbolic paths with the Sun at one focus,
such comets pass by the Sun only one time unlike those in elliptical orbits,
which reappear at intervals.
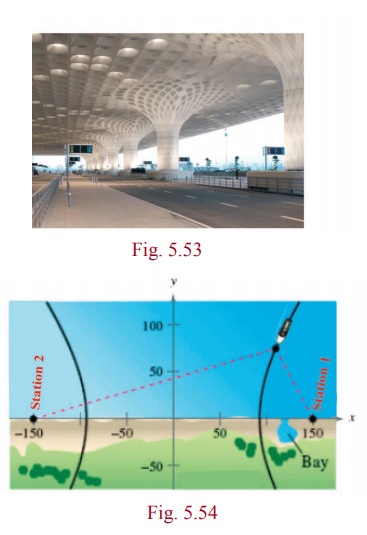
We also see hyperbolas in architecture, such as Mumbai Airport
terminal (Fig. 5.53), incross section of a planetarium, an locating ships (Fig.
5.54), or a cooling tower for a steam or nuclear power plant. (Fig. 5.5)
Example 5.30
A semielliptical archway over a one-way road has a height of 3m
and a width of 12m . The truck has a width of 3m and a height
of 2.7m . Will the truck clear the opening of the archway? (Fig.
5.6)
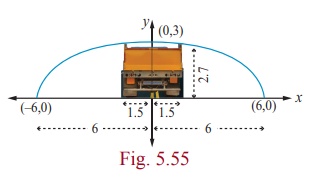
Solution
Since the truck’s width is 3m , to determine the
clearance, we must find the height of the archway 1.5m from the
centre. If this height is 2.7m or less the truck will not clear the
archway.
From the diagram a = 6 and b = 3 yielding the equation
of elipse as 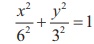 .
.
The edge of the 3m wide truck corresponds to x =
1.5m
from centre We will find the height of the archway 1.5m from the centre by substituting x = 1.5
and solving for y
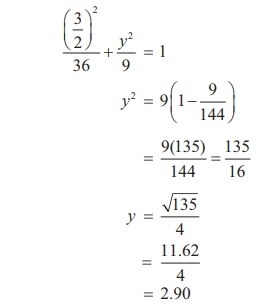
Thus the height of arch way 1.5m from the centre is
approximately 2.90m . Since the truck’s height is 2.7m , the
truck will clear the archway.
Example 5.31
The maximum and minimum distances of the Earth from the Sun
respectively are 152 ×106 km and 94.5×106 km. The Sun is
at one focus of the elliptical orbit. Find the distance from the Sun to the
other focus.
Solution
AS = 94.5×106 km, SA ' = 152 ×106 km
a + c = 152 ×106
a − c = 94.5×106
Subtracting 2c = 57.5×106 = 575×105
km
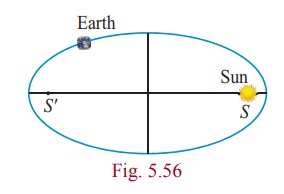
Distance of the Sun from the other focus is SS′ = 575×105
km.
Example 5.32
A concrete bridge is designed as a parabolic arch. The road over
bridge is 40m long and the maximum height of the arch is 15m .
Write the equation of the parabolic arch.
Solution
From the graph the vertex is at (0, 0) and the parabola is open
down
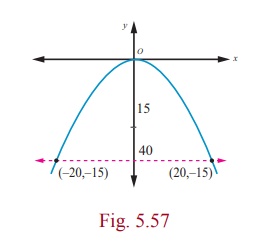
Equation of the parabola is x2 = −4ay
(−20, −15) and (20, −15) lie on the parabola
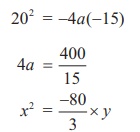
Therefore equation is 3x2=-80y
Example 5.33
The parabolic communication antenna has a focus at 2m distance
from the vertex of the antenna.
Find the width of the
antenna 3m from the vertex.
Solution
Let the parabola be y2 = 4ax .
Since focus is 2m from the vertex a = 2
Equation of the parabola is y2 = 8x

Let P be a point on the parabola whose x -coordinate is 3m from the vertex P (3, y)
y2 = 8´ 3
y = √(8x3)
= 2√6
The width of the antenna 3m
from the vertex is 4√6 m.
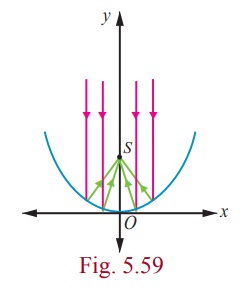
4. Reflective property of parabola
The light or sound or radio waves originating at a parabola’s
focus are reflected parallel to the parabola’s axis (Fig. 5.60) and conversely
the rays arriving parallel to the axis are directed towards the focus (Fig.
5.59).
Example 5.34
The equation y = (1/32) x2 models cross
sections of parabolic mirrors that are used for solar energy. There is a heating
tube located at the focus of each parabola; how high is this tube located above
the vertex of the parabola?
Solution
Equation of the parabola is
y = (1/32) x2
That is x2
= 32y ; the vertex is (0, 0)
= 4(8) y
⇒ a = 8
So the heating tube needs to be placed at focus (0, a) .
Hence the heating tube needs to be placed 8 units above the vertex of the
parabola.
Example 5.35
A search light has a parabolic reflector (has a cross section that
forms a ‘bowl’). The parabolic bowl is 40 cm wide from rim to rim and 30 cm deep.
The bulb is located at the focus .
(1) What is the equation of the parabola used
for reflector?
(2) How far from the vertex is the bulb to be
placed so that the maximum distance covered?
Solution
Let the vertex be (0, 0) .
The equation of the parabola is
y2 = 4ax
(1) Since the diameter is 40 cm and the depth is 30 cm , the point (30,20) lies on the parabola.
202 = 4a ´ 30
4a = 400/30 = 40/3 .
Equation is y2 = 40/3 x.
(2) The bulb is at focus (0, a)
. Hence the bulb is at a distance of 10/3 cm from the vertex.
Example 5.36
An equation of the elliptical part of an optical lens system is 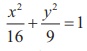 .
.
The parabolic part of the system has a focus in common with the
right focus of the ellipse .The vertex of the parabola is at the origin and the
parabola opens to the right. Determine the equation of the parabola.
Solution

In the given ellipse a2 = 16 , b2
= 9
then c2 = a2 - b2
c2 = 16 – 9
= 7
c = ± √7
Therefore the foci are F ( √7, 0), F ¢(-√7, 0) . The focus of the parabola is (√7, 0) ⇒ a =√7 Equation of the parabola is y2 = 4√7x .
5. Reflective Property of an Ellipse
The lines from the foci to a point on an ellipse make equal
angles with the tangent line at that point (Fig. 5.62).

The light or sound or radio waves emitted from one focus hits any point P on the ellipse is received at the other focus (Fig. 5.63).
Example 5.37
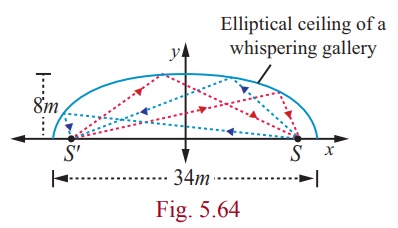
A room 34m long is constructed to be a whispering
gallery. The room has an elliptical ceiling, as shown in Fig. 5.64. If the
maximum height of the ceiling is 8m , determine where the foci are
located.
Solution
The length a of the semi major axis of the elliptical
ceiling is 17m . The height b of the semi minor axis is 8m .
Thus
c2
= a2 - b2 = 172 - 82
then
c = √[289 – 64] = √225
=
15
For the elliptical ceiling the foci are located on either side
about 15m from the centre, along its major axis.
A non-invasive medical miracle
In a lithotripter, a high-frequency sound wave is emitted from a
source that is located at one of the foci of the ellipse. The patient is placed
so that the kidney stone is located at the other focus of the ellipse.
Example 5.38
If the equation of the ellipse is  ( x and y
are measured in centimeters) where to the nearest centimeter, should the
patient’s kidney stone be placed so that the reflected sound hits the kidney
stone?
( x and y
are measured in centimeters) where to the nearest centimeter, should the
patient’s kidney stone be placed so that the reflected sound hits the kidney
stone?
Solution
The equation of the ellipse is  .
.
The origin of the sound wave and the kidney stone of patient should be at the foci in order to crush the stones.
a2 = 484 and b2 = 64
c2 = a2 - b2
= 484 -64
= 420
c ≈ 20.5
Therefore the patient’s kidney stone should be placed 20.5cm
from the centre of the ellipse.
6. Reflective Property of a Hyperbola
The lines from the foci to a point on a hyperbola make equal
angles with the tangent line at that point (Fig. 5.66).
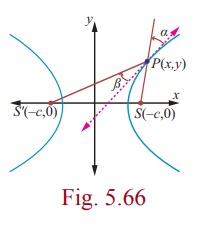
The light or sound or radio waves directed from one focus is received at the other focus as in the case ellipse (Fig. 5.54) used in spotting location of ships sailing in deep sea.
Example 5.39
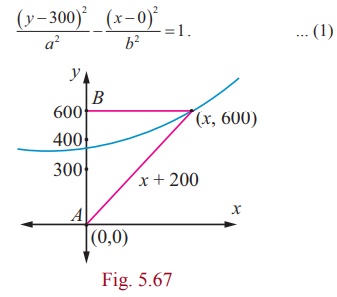
Two coast guard stations are located 600 km apart at points A(0,
0) and B(0, 600) . A distress signal from a ship at P is received
at slightly different times by two stations. It is determined that the ship is
200 km farther from station A than it is from station B .
Determine the equation of hyperbola that passes through the location of the
ship.
Solution
Since the centre is located at (0, 300) , midway between the two
foci,which are the coast guard stations, the equation is
To determine the values of a and b , select two points
known to be on the hyperbola and substitute each point in the above equation.
The point (0, 400) lies on the hyperbola, since it is 200 km
further from Station A than from station B .
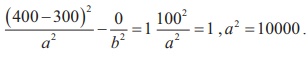
There is also a point (x, 600) on the
hyperbola such that 6002 + x2 = ( x
+ 200)2.
360000 + x2
= x2 + 400x + 40000
x = 800
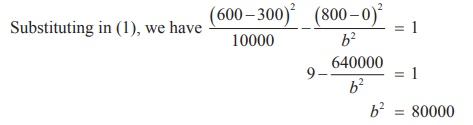
Thus the required equation of the hyperbola is
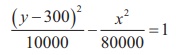
The ship lies somewhere on this hyperbola. The exact location
can be determined using data from a third station.
Example 5.40
Certain telescopes contain both parabolic mirror and a
hyperbolic mirror. In the telescope shown in figure 5.68 the parabola and
hyperbola share focus F1 which is 14m above the vertex
of the parabola. The hyperbola’s second focus F2 is 2m above
the parabola’s vertex. The vertex of the hyperbolic mirror is 1m below F1.
Position a coordinate system with the origin at the centre of the hyperbola and
with the foci on the y -axis. Then find the equation of the hyperbola.
Solution
Let V1 be the vertex of the parabola and V2
be the vertex of the hyperbola.
![]() = 14 - 2 = 12m, 2c = 12, c = 6
= 14 - 2 = 12m, 2c = 12, c = 6
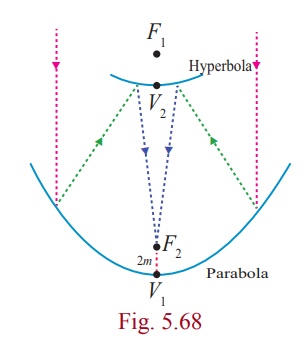
The distance of centre to the vertex of the hyperbola is a = 6 −1 = 5
b2 = c2 - a2
= 36 - 25 = 11.
Therefore the equation of the hyperbola is y2/25 - x2/11 = 1
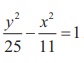
Related Topics