Problem Questions with Answer, Solution - Exercise 5.1: Circle | 12th Mathematics : UNIT 5 : Two Dimensional Analytical Geometry II
Chapter: 12th Mathematics : UNIT 5 : Two Dimensional Analytical Geometry II
Exercise 5.1: Circle
EXERCISE 5.1
1. Obtain the equation of the circles with radius 5 cm and touching x-axis at the origin in general form.

2. Find the equation of the circle with centre (2, −1) and passing through the point (3, 6) in standard form.

3. Find the equation of circles that touch both the axes and pass through (−4, −2) in general form.

4. Find the equation of the circle with centre (2, 3) and passing through the intersection of the lines 3x − 2 y −1 = 0 and 4x + y − 27 = 0 .

5. Obtain the equation of the circle for which (3, 4) and (2, −7) are the ends of a diameter.

6. Find the equation of the circle through the points (1, 0), (−1, 0) , and (0,1) .

7. A circle of area 9π square units has two of its diameters along the lines x + y = 5 and x − y = 1. Find the equation of the circle.

8. If y = 2√2x + c is a tangent to the circle x2 + y2 = 16 , find the value of c .
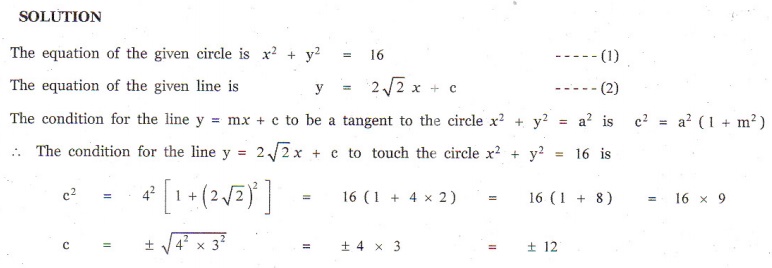
9. Find the equation of the tangent and normal to the circle x2 + y2 − 6x + 6 y − 8 = 0 at (2, 2) .

10. Determine whether the points (−2,1), (0, 0) and (−4, −3) lie outside, on or inside the circle x2 + y2 − 5x + 2 y − 5 = 0 .

11. Find centre and radius of the following circles.
(i) x2 + ( y + 2)2 = 0
(ii) x2 + y2 + 6x - 4 y + 4 = 0
(iii) x2 + y2 - x + 2 y - 3 = 0
(iv) 2x2 + 2 y2 − 6x + 4 y + 2 = 0

12. If the equation 3x2 + (3 − p) xy + qy2 − 2 px = 8 pq represents a circle, find p and q . Also determine the centre and radius of the circle.

Answers:
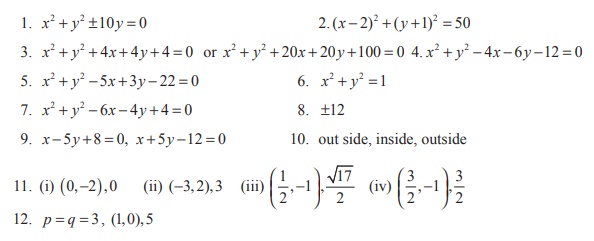
Related Topics