Parabola

Parabola

Since e = 1 , for a parabola, we note that the parabola is the locus of points in a plane that are equidistant from both the directrix and the focus.

(i) Equation of a parabola in standard form with vertex at (0, 0)

Let S be the focus and l be the directrix.

Draw SZ perpendicular to the line l .

Let us assume SZ produced as x -axis and the perpendicular bisector of SZ produced as y - axis. The intersection of this perpendicular bisector with SZ be the origin O .

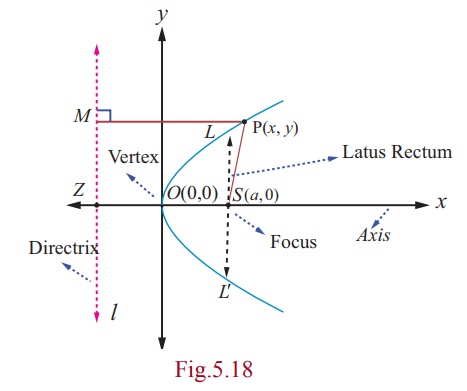
Let SZ = 2a . Then S is (a, 0) and the equation of the directrix is x + a = 0 .

Let P(x, y) be the moving point in the locus that yield a parabola. Draw PM perpendicular to the directrix. By definition, e = SP/PM = 1. So, SP² = PM² .

Then, (x - a)² + y² = (x + a)². On simplifying, we get y² = 4ax which is the equation of the parabola in the standard form.

The other standard forms of parabola are y² = -4ax, x² = 4ay , and x² = -4ay .

Definition 5.3

·            The line perpendicular to the directrix and passing through the focus is known as the Axis of the parabola.

·            The intersection point of the axis with the curve is called vertex of the parabola

·            Any chord of the parabola, through its focus is called focal chord of the parabola

·            The length of the focal chord perpendicular to the axis is called latus rectum of the parabola

Example 5.14

Find the length of Latus rectum of the parabola y² = 4ax .

Solution

Equation of the parabola is y² = 4ax.

Latus rectum LL¢ passes through the focus (a, 0) . Refer (Fig.5.18)

Hence the point L is (a, y₁) .

Therefore y₁² = 4a².

Hence y₁ = ± 2a .

The end points of latus rectum are (a, 2a) and (a, -2a) .

Therefore length of the latus rectum LL¢ = 4a .

Note

The standard form of the parabola y² = 4ax has for its vertex (0, 0) , axis as x -axis, focus as (a, 0) . The parabola y² = 4ax lies completely on the non-negative side of the x-axis. Replacing y by –y in y² = 4ax, the equation remains the same. so the parabola y² = 4ax is symmetric about x-axis; that is, x-axis is the axis and symmetry of y² = 4ax

(ii) Parabolas with vertex at (h, k )

When the vertex is (h, k) and the axis of symmetry is parallel to x -axis, the equation of the parabola is either ( y - k )² = 4a(x - h) or ( y - k )² = - 4a(x - h) (Fig. 5.19, 5.20).

When the vertex is (h, k) and the axis of symmetry is parallel to y -axis, the equation of the parabola is either (x - h)² = 4a( y - k ) or (x - h)² = - 4a( y - k ) (Fig. 5.21, 5.22).