Ellipse

Ellipse

We invoke that an ellipse is the locus of a point which moves such that its distance from a fixed point (focus) bears a constant ratio (eccentricity) less than unity its distance from its directrix bearing a constant ratio e (0 < e < 1) .

(i) Equation of an Ellipse in standard form

Let S be a focus, l be a directrix, e be the eccentricity ( 0 < e < 1) and P(x, y) be the moving point. Draw SZ and PM perpendicular to l .

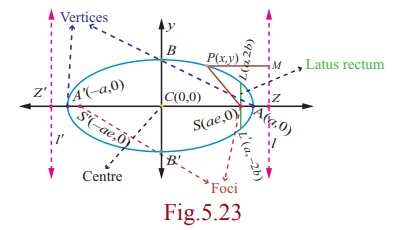
Let A and A′ be the points which divide SZ internally and externally in the ratio e :1 respectively. Let AA′ = 2a . Let the point of intersection of the perpendicular bisector with AA′ be C. Therefore CA = a and CA′ = a. Choose C as origin and CZ produced as x -axis and the perpendicular bisector of AA′ produced as y –axis.

By definition,

Hence we obtain the locus of P as 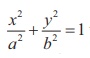  which is the equation of an ellipse in standard form and note that it is symmetrical about x and y axis.

Definition 5.4

(1) The line segment AA¢ is called the major axis of the ellipse and is of length 2a .

(2) The line segment BB¢ is called the minor axis of the ellipse and is of length 2b .

(3) The line segment CA = the line segment CA¢ = semi major axis = a and the line segment CB = the line segment CB¢ = semi minor axis = b.

(4) By symmetry, taking S¢(-ae, 0) as focus and x =- a/e as directrix l¢ gives the same ellipse.

Thus, we see that an ellipse has two foci, S (ae, 0) and S¢(-ae, 0) and two vertices A(a, 0) and A¢(-a, 0) and also two directrices, x = a/e and x =- a/e.

Example 5.15

Find the length of Latus rectum of the ellipse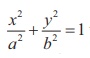 

Solution

The Latus rectum LL’ (Fig. 5.22) of an ellipse 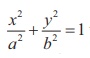passes through S (ae, 0) .

Hence  L  is (ae, y₁ ) .

Therefore,

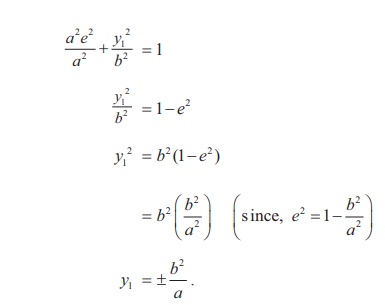
That is, the end points of Latus rectum L and L′ are 

Hence the length of latus rectum LL' = 2b² / a

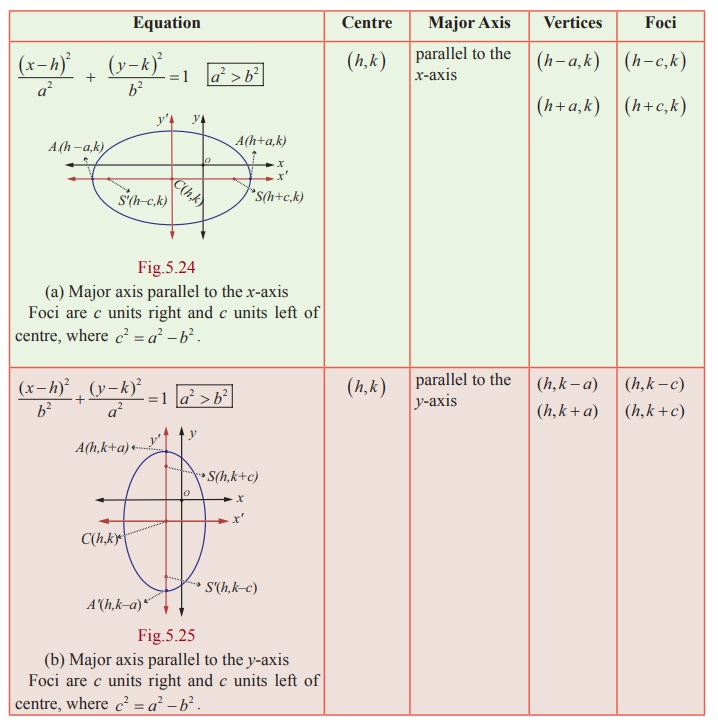
(iii) Types of ellipses with centre at (h, k )

(a) Major axis parallel to the x-axis

From Fig. 5.24

The length of the major axis is 2a . The length of the minor axis is 2b . The coordinates of the vertices are (h + a, k ) and (h − a, k ) , and the coordinates of the foci are (h + c, k ) and (h − c, k ) where c² = a² − b².

(b) Major axis parallel to the y-axis

From Fig. 5.25

The length of the major axis is 2a . The length of the minor axis is 2b. The coordinates of the vertices are  (h, k + a) and (h, k – a) , and the coordinates of the foci are (h, k + c) and (h, k – c) , where c² = a² - b² .

Theorem 5.5

The sum of the focal distances of any point on the ellipse is equal to length of the major axis.

Proof

Let P(x, y) be a point on the ellipse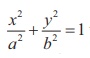 

Draw MM ¢ through P  perpendicular to directrices l and l¢ .

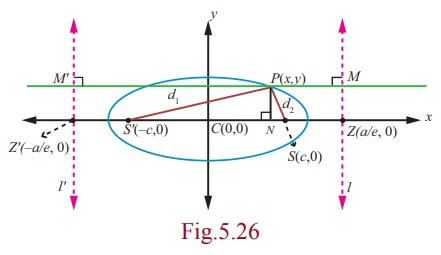
Draw PN ^ to x -axis.

By definition SP = ePM

= eNZ

= e[CZ - CN ]

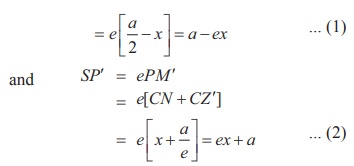
Hence, SP + S¢P = a - ex + a + ex = 2a

Remark

When b = a , the equation 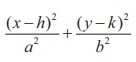 = 1, becomes (x - h)² + ( y - k )² = a² the equation of circle with centre (h, k) and radius a .

When b = a, e = 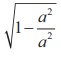 = 0 . Hence the eccentricity of the circle is zero.

Furthere, SP/ PM = 0 implies PM →∞ . That is, the directrix of the circle is at infinity.

Remark

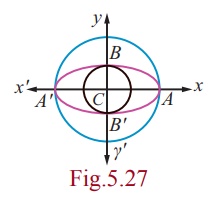
Auxiliary circle or circumcircle is the circle with length of major axis as diameter and Incircle is the circle with length of minor axis as diameter. They are given by x² + y² = a² and x² + y² = b² respectively.