Hyperbola

Hyperbola

We invoke that a hyperbola is the locus of a point which moves such that its distance from a fixed point (focus) bears a constant ratio (eccentricity) greater than unity its distance from its directrix, bearing a constant ratio e (e > 1) .

(i) Equation of a Hyperbola in standard form with centre at (0, 0)

Let S be a focus, l be the directrix line, e be the eccentricity e > 1 and P(x, y) be the moving point. Draw SZ and PM perpendicular to l .

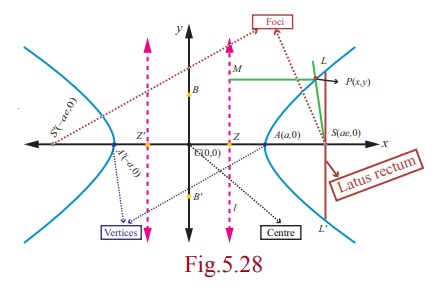
Let A and A′ be the points which divide SZ internally and externally in the ratio e :1 respectively.

Let AA′ = 2a . Let the point of intersection of the perpendicular bisector with AA′ be C . Then CA= CA' = a Choose C as origin and the line CZ produced as x -axis and the perpendicular bisector of AA′ as y -axis.

Þ AS = eAZ         A¢S = eA¢Z

Þ CS - CA = e(CA - CZ )                 A¢C + CS = e( A¢C + CZ )

Þ CS - a = e(a - CZ ) … (1)                 a + CS = e(a + CZ ) … (2)

(1) + (2) gives CS = ae and (2) - (1) gives CZ = a/e.

Hence, the coordinates of S are (ae, 0) . Since PM = x – a/e , the equation of directrix is x – a/e = 0 . Let P(x, y) be any point on the hyperbola.

By the definition of a conic, SP/ PM = e

 Þ SP² = e²PM².

Then (x - ae)² + ( y - 0)² = e² ( x – a/e )²

Þ (x - ae)² + y² = (ex - a)²

Þ (e² -1)x² - y² = a² (e² -1)

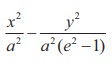 =  1. Since e > 1, a² (e²  -1) > 0 . Setting  a²(e²  -1) = b², we obtain the locus of P  as x²/a² - y²/b² = 1 =  which is the equation of a Hyperbola in standard form and  note that it is symmetrical about x and y-axes.

Taking ae = c , we get b² = c² - a² .

Definition 5.5

(1) The line segment AA′ is the transverse axis of length 2a .

(2) The line segment BB′ is the conjugate axis of length 2b .

(3) The line segment CA = the line segment CA′ = semi transverse axis = a and the line segment CB = the line segment CB′ = semi conjugate axis = b .

(4) By symmetry, taking S′(−ae, 0) as focus and x =− a/e as directrix l′ gives the same hyperbola.

Thus we see that a hyperbola has two foci S (ae, 0) and S¢(-ae, 0) , two vertices A(a, 0)

and A¢(-a, 0) and two directrices x = a/e and x =- a/e.

Length of latus rectum of hyperbola is 2b² / a, which can be obtained along lines as that of the ellipse.

Asymptotes

Let P(x, y) be a point on the curve defined by y = f (x) , which moves further and further away from the origin such that the distance between P and some fixed line tends to zero. This fixed line is called an asymptote.

Note that the hyperbolas admit asymptotes while parabolas and ellipses do not.

(ii) Types of Hyperbola with centre at (h, k)

Remark

(1) The circle described on the transverse axis of hyperbola as its diameter is called the auxiliary circle of the hyperbola. Its equation is x² + y² = a².

(2) The absolute difference of the focal distances of any point on the hyperbola is constant and is equal to length of transverse axis. That is, | PS - PS¢ | = 2a . (can be proved similar that of ellipse)

So far we have discussed four standard types of parabolas, two types of ellipses and two types of hyperbolas. There are plenty of parabolas, ellipses and hyperbolas whose equations cannot be classified under the standard types, For instance consider the following parabola, ellipse, and hyperbola.

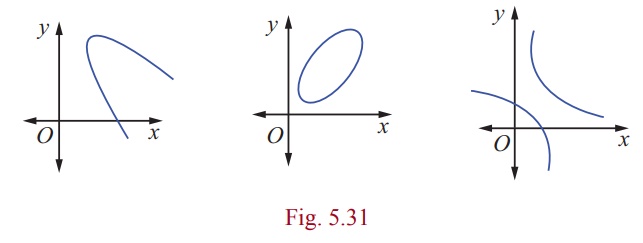
By a suitable transformation of coordinate axes they can be represented by standard equations.

Example 5.14

Find the equation of the parabola with focus (− √2, 0) and directrix x = √2.

Solution

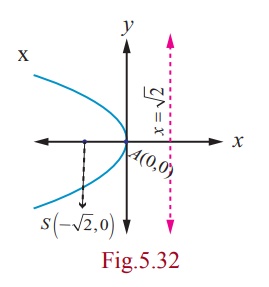
Parabola is open left and axis of symmetry as x-axis and vertex (0, 0).

Then the equation of the required parabola is

(y - 0)² = - 4√2 ( x - 0)

 ⇔ y² = - 4√2x.

Example 5.15

Find the equation of the parabola whose vertex is (5, -2) and focus (2, -2).

Solution

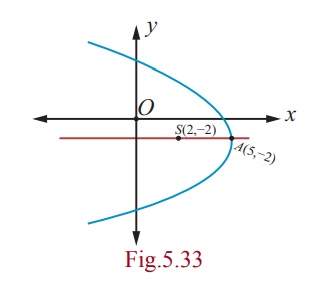
Given vertex A(5, -2) and focus S(2, -2) and the focal distance AS = a = 3 .

Parabola is open left and symmetric about the line parallel to x -axis.

Then, the equation of the required parabola is

( y + 2)² = -4 (3)( x - 5)

⇔ y² + 4 y + 4 = -12x + 60

⇔ y² + 4 y +12x - 56 = 0 .

Example 5.16

Find the equation of the parabola with vertex (-1, -2) , axis parallel to y -axis and passing through (3, 6) .

Solution

Since axis is parallel to y -axis the required equation of the parabola is

( x +1)² = 4a ( y + 2) .

Since this passes through (3,6), we get

(3 +1)² = 4a (6 + 2)

⇔ a = 1/2.

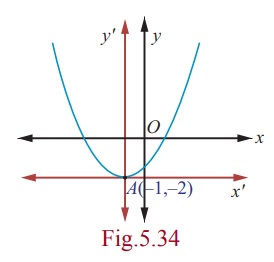
Then the equation of parabola is ( x +1)² = 2 ( y + 2) which on simplifying yields,

x² + 2x - 2y - 3 = 0 .

Example 5.17

Find the vertex, focus, directrix, and length of the latus rectum of the parabola x² - 4x - 5 y -1 = 0.

Solution

For the parabola,

x² - 4x - 5y -1 = 0

⇔ x² - 4x = 5y +1

⇔ x² - 4x + 4 = 5y +1+ 4 .

⇒ ( x - 2)² = 5( y +1) which is in standard form. Therefore, 4a = 5 and the vertex is (2, -1) , and the focus is ( 2, 1/4 ) .

Equation of directrix is y + k + a = 0

y -1+ 5/4 = 0

4y +1 = 0 .

Length of latus rectum 5 units. 

Example 5.18

Find the equation of the ellipse with foci (± 2, 0) , vertices (± 3, 0) .

Solution

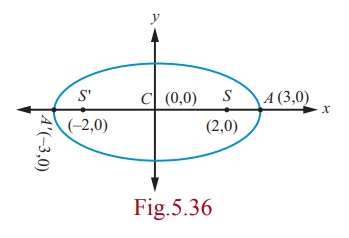
From Fig. 5.36, we get

SS′  =  2c and 2c = 4; A′A = 2a = 6

⇒ c  =  2 and a = 3 ,

⇒ b² = a² − c² = 9 − 4 = 5 .

Major axis is along x -axis, since a > b .

Centre is (0, 0) and Foci are (±2, 0) .

Therefore, equation of the ellipse is x²/9 + y²/5 = 1

Example 5.19

Find the equation of the ellipse whose eccentricity is  ½, one of the foci is (2, 3) and a directrix is x = 7 . Also find the length of the major and minor axes of the ellipse.

Solution

By the definition of a conic, SP/PM= e or SP² = e² PM ².

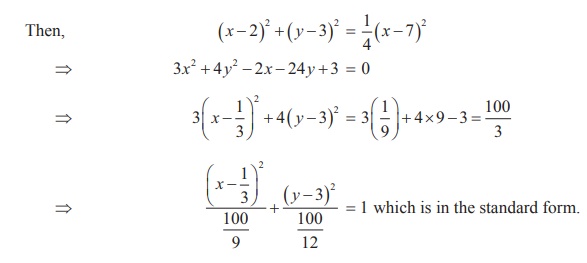
Therefore, the length of major axis = 2a = 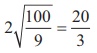 and

the length of minor axis = 2b = 

Example 5.20

Find the foci, vertices and length of major and minor axis of the conic

4x² + 36 y² + 40x − 288 y + 532 = 0 .

Solution

Completing the square on x and y of 4x² + 36y² + 40x - 288y + 532 = 0 ,

4(x² +10x + 25 - 25) + 36( y² - 8 y +16 -16) + 532 = 0 , gives

4(x² +10x + 25 ) + 36( y² - 8 y +16 ) = -532 +100 + 576

4 ( x + 5)²  + 36 ( y - 4)² = 144 . 

Dividing both sides by 144 , the equation reduces to

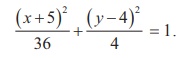
This is an ellipse with centre (−5, 4) , major axis is parallel to x -axis, length of major axis is 12 and length of minor axis is 4. Vertices are (1, 4) and (−11, 4) .

Now,  c²  = a² − b² = 36 − 4 = 32

and  c =  ±4√2.

Then the foci are (-5 - 4√2, 4) and (-5 + 4√2, 4).

Length of the major axis = 2a = 12 units and

the length of the minor axis = 2b = 4 units.

Example 5.21

For the ellipse 4x² + y² + 24x − 2 y + 21 = 0 , find the centre, vertices, and the foci. Also prove that the length of latus rectum is 2 .

Solution 

Rearranging the terms, the equation of ellipse is 

4x² + 24x + y² − 2 y + 21 = 0

That is,  4 (x²  + 6x + 9 − 9) + ( y²  − 2 y +1−1) + 21  =  0 ,

4 ( x + 3)²  − 36 + ( y −1)²  −1+ 21  =  0 ,

4 ( x + 3)²  + ( y −1)²  = 16 ,

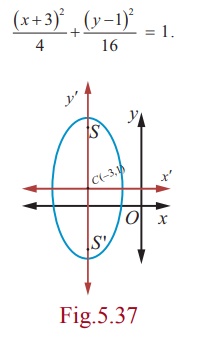
Centre is (−3,1) a = 4, b = 2 , and the major axis is parallel to y -axis 

c²  = 16 - 4 = 12

c =  ±2√3.

 Therefore, the foci are (-3, 2√3 +1) and (-3, -2√3+1) 

Vertices are (1,  ±4 +1) . That is the vertices are (1, 5) and (1, -3) , and the length of Latus rectum = 2b² / a = 2 units. (see Fig. 5.37)

Example 5.22

Find the equation of the hyperbola with vertices (0, ±4) and foci (0, ±6) .

Solution 

From Fig. 5.38, the midpoint of line joining foci is the centre C(0,0).

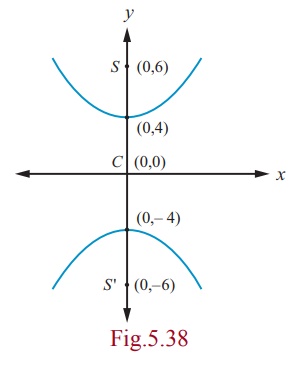
Transverse axis is y -axis 

AA¢  = 2a ⇒ 2a = 8,

SS¢ = 2c = 12, c = 6

a = 4

b² = c² - a² = 36 -16 = 20 .

Hence the equation of the required hyperbola is y²/16 - x²/20 =  1 =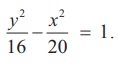 

Example 5.23

Find the vertices, foci for the hyperbola 9x² −16y² = 144 .

Solution

Reducing 9x² −16 y²= 144 to the standard form,  

We have,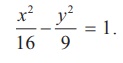 

With the transverse axis is along x -axis vertices are (−4, 0) and (4, 0) ;

and c² = a² + b² = 16 + 9 = 25 , c = 5 .

Hence the foci are (−5, 0) and (5, 0) .

Example 5.24

Find the centre, foci, and eccentricity of the hyperbola 11x² − 25 y² − 44x + 50 y − 256 = 0

Solution

Rearranging terms in the equation of hyperbola to bring it to standard form,

we have, 11(x² − 4x) − 25( y² − 2 y) − 256 = 0

11( x − 2)²  − 25( y −1)² = 256 − 44 + 25

11( x − 2)²  − 25( y −1)²  = 275

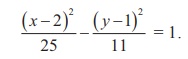
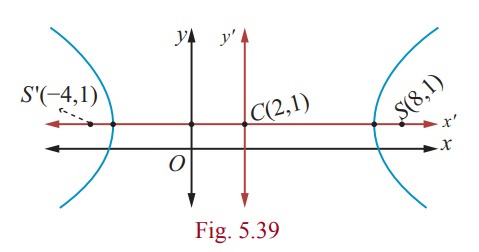
Centre (2,1) , a²  = 25, b²  = 11

c² = a²  + b²

= 25 +11 = 36

Therefore, c =  ±6

and e = c/a = 6 and the coordinates of foci are (8,1) and (-4,1) from Fig. 5.39.

Example 5.25

The orbit of Halley’s Comet (Fig. 5.51) is an ellipse 36.18 astronomical units long and by 9.12 astronomical units wide. Find its eccentricity.

Solution

Given that 2a = 36.18, 2b = 9.12 , we get

Note

One astronomical unit (mean distance of Sun and earth) is 1, 49, 597,870 km , the semi major axis of the Earth’s orbit.