Equation, Definition, Theorem, Proof, Solved Example Problems - Tangents and Normals to Conics | 12th Mathematics : UNIT 5 : Two Dimensional Analytical Geometry II
Chapter: 12th Mathematics : UNIT 5 : Two Dimensional Analytical Geometry II
Tangents and Normals to Conics
Tangents and Normals to Conics
Tangent to a plane curve is a straight line touching the curve at
exactly one point and a straight line perpendicular to the tangent and passing
through the point of contact is called the normal at that point.
1. Equation of tangent and normal to the parabola y2 = 4ax
(i) Equation of tangent in cartesian form
Let P ( x1 , y1 ) and
Q ( x2 , y2 ) be two points on a
parabola y2 = 4ax .
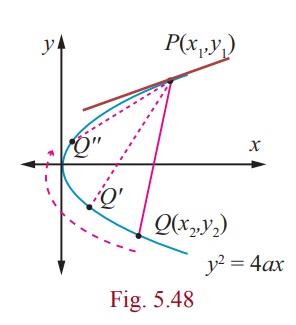
Then, y12
= 4ax1 and
y22
= 4ax2,
and y12 – y22 = 4a(x1 – x2).
Simplifying, 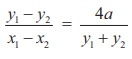 , the slope of the chord PQ.
, the slope of the chord PQ.
Thus 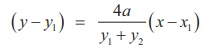 , represents
the equation of the chord PQ.
, represents
the equation of the chord PQ.
When Q → P , or y2 → y1
the chord becomes tangent at P.
Thus the equation of tangent at (x1 , y1)
is
y – y1 = 4a/2y1 (x - x1)
where 2a/y1 is the slope
of the tangent ... (1)
yy1 – y12 = 2ax - 2ax1
yy1 - 4ax1 = 2ax - 2ax1
yy1 = 2a ( x + x1)
(ii) Equation of tangent in parametric form
Equation of tangent at (at2 , 2at) on
the parabola is
y(2at) = 2a(x + at2)
yt = x + at2
(iii) Equation of normal in cartesian form
From (1) the slope of normal is − y11/2a
Therefore equation of the normal is
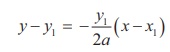
2ay − 2ay1 = − y1x
+ y1x1
xy1 + 2ay = y1( x1 + 2a)
xy1 + 2ay = x1y1
+ 2ay1
(iv) Equation of normal in parametric form
Equation of the normal at (at2 , 2at)
on the parabola is
x2at + 2ay = at2 (2at) + 2a(2at)
2a(xt + y) = 2a(at3
+ 2at)
y + xt = at 3 + 2at
Theorem 5.6
Three normals can be drawn to a parabola y2 =
4ax from a given point, one of which is always real.
Proof
y2 = 4ax is the given parabola. Let (α, β) be
the given point.
Equation of the normal in parametric form is
y = – tx + 2at + at3 ... (1)
If m is the slope of the normal then m = −t .
Therefore the equation (1) becomes y = mx − 2am
− am3.
Let it passes through (α, β) , then
β = ma − 2am − am3
am3 + (2a − α)m + β = 0
which being a cubic equation in m , has three values of m
. Consequently three normals, in general, can be drawn from a point to the
parabola, since complex roots of real equation, always occur in conjugate pairs
and (1) being an odd degree equation, it has atleast one real root. Hence
atleast one normal to the parabola is real.
2. Equations of tangent and normal to Ellipse and Hyperbola (the proof of the following are left to the reader)
(1) Equation of the tangent to the ellipse 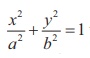
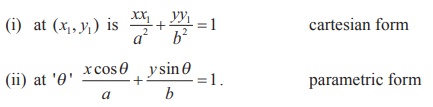
(2) Equation of the normal to the ellipse 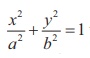
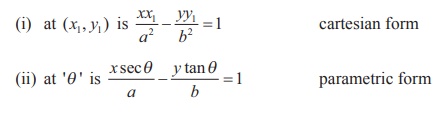
(3) Equation of the tangent to the hyperbola 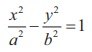
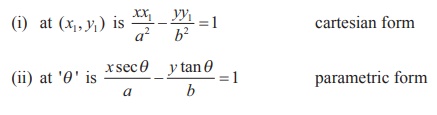
(4) Equation of the normal to the hyperbola 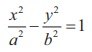

3. Condition for the line y =
mx + c to
be a tangent to the conic sections
(i) parabola y2 = 4ax
Let (x1 , y1 ) be the point
on the parabola y2 = 4ax . Then y12
= 4ax1 … (1)
Let y = mx + c be the tangent to the
parabola ..
(2)
Equation of tangent at ( x1 , y1
) to the parabola from 5.6.1 is yy1 = 2a ( x +
x1 ) …. (3)
Since (2) and (3) represent the same line, coefficients are
proportional.

So the point of contact is ( a/m2 , 2a/m ) and the equation of
tangent to parabola is y = mx + a/m .
The condition for the line y = mx + c to be tangent to the ellipse or hyperbola can be derived as follows in the same way as in the case of parabola.
(ii) ellipse 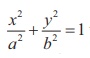
Condition for line y = mx +
c to be the tangent to the ellipse 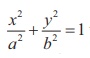 is c2 = a2m2
+ b, with the point of contact is
is c2 = a2m2
+ b, with the point of contact is 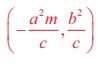 and the equation of
tangent is y = mx ± √[a2m2+b2] =
and the equation of
tangent is y = mx ± √[a2m2+b2] = 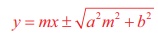 .
.
(iii) Hyperbola 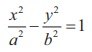
Condition for line y = mx +
c to be the tangent to the hyperbola 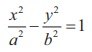 is c2 = a2m2 – b2, with the point of contact is
is c2 = a2m2 – b2, with the point of contact is 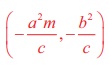 and the equation of tangent is y = mx ± √[a2m2
- b2]
=
and the equation of tangent is y = mx ± √[a2m2
- b2]
=  .
.
Note
(1) In y = mx ± 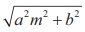 , either y = mx +
, either y = mx + 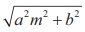 or y =
mx –
or y =
mx – 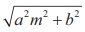 is the equation to the tangent of ellipse but not both.
is the equation to the tangent of ellipse but not both.
(2) In y = mx ± 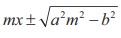 , either y = mx +
, either y = mx + 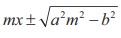 or y = mx –
or y = mx – 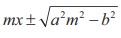 is the
equation to the tangent of hyperbola but not both.
is the
equation to the tangent of hyperbola but not both.
Results (Proof, left to the reader)
(1) Two tangents can be drawn to (i) a parabola (ii) an ellipse
and (iii) a hyperbola, from any external point on the plane.
(2) Four normals can be drawn to (i) an ellipse and (ii) a
hyperbola from any external point on the plane.
(3) The locus of the point of intersection of perpendicular
tangents to
(i) the parabola y2 = 4ax is x =
−a
(the directrix).
(ii) the ellipse 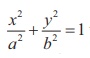 ( called the director circle
of ellipse).
( called the director circle
of ellipse).
(iii) the hyperbola 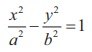 (called director
circle of hyperbola).
(called director
circle of hyperbola).
Example 5.27
Find the equations of tangent and normal to the parabola x2
+ 6x + 4 y + 5 = 0 at (1, −3).
Solution
Equation of parabola is x2 + 6x + 4 y +
5 = 0 .
x2 + 6x + 9 − 9 + 4 y + 5 = 0
(x + 3)2 = −4( y −1)
Let X = x + 3,Y = y −1
Equation (1) takes the standard form
X2 = −4Y
Equation of tangent is XX1 = −2(Y + Y1
)
At (1, −3) X1 = 1+ 3 = 4; Y1
= −3 −1 = −4
Therefore, the equation of tangent at (1, −3) is
(x + 3)4 = −2( y −1− 4)
2x + 6 = − y + 5 .
2x + y +1 = 0 .
Slope of tangent at (1, −3) is −2 , so slope of normal at (1,
−3) is ½
Therefore, the equation of normal at (1, −3) is given by
y + 3 = 1/2 (x−1)
2 y + 6 = x −1
x − 2 y − 7 = 0 .
Example 5.28
Find the equations of tangent and normal to the ellipse x2
+ 4 y2 = 32 when θ = π/4.
Solution
Equation of ellipse is x2 + 4y2=
32

Aliter
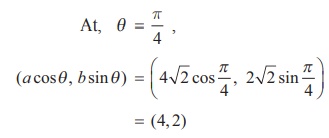
= (4, 2)
Equation of tangent at θ = π/4 is same at ( 4, 2).
Equation of tangent in cartesian form is 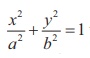
x + 2 y
- 8 = 0
Slope of tangent is – 1/2
Slope of normal is 2
Equation of normal is y - 2
= 2(x - 4)
y - 2x + 6 = 0.
Related Topics