Summary

SUMMARY

(1)      Equation of the circle in a standard form is (x - h)² + ( y - k )² = r ² .

(i)        Centre (h, k) (ii) radius ‘ r ’

(2)      Equation of a circle in general form is x² + y² + 2gx + 2 fy + c = 0 .

(i)        centre (-g, - f ) (ii) radius = √[g ² + f ² – c]

(3)      The circle through the intersection of the line lx + my + n = 0 and the circle

x² + y² + 2gx + 2 fy + c = 0 is x² + y² + 2gx + 2 fy + c + λ(lx + my + n) = 0, λ ∈  R¹ .

(4)      Equation of a circle with (x₁ , y₁ ) and (x₂ , y₂ ) as extremities of one of the diameters is

(x - x₁)(x - x₂ ) + ( y - y₁ )( y - y₂ ) = 0 .

(5)      Equation of tangent at (x₁ , y₁ ) on circle x² + y² + 2gx + 2fy + c = 0 is

xx₁ + yy₁ + g(x + x₁ ) + f ( y + y₁ ) + c = 0

(6)      Equation of normal at (x₁ , y₁ ) on circle x² + y² + 2gx + 2 fy + c = 0 is

yx₁ - xy₁ + g( y - y₁ ) - f (x - x₁) = 0 .

Table 1

Tangent and normal

Table 2

Condition for the sine  y = mx + c to be a tangent to the Conics

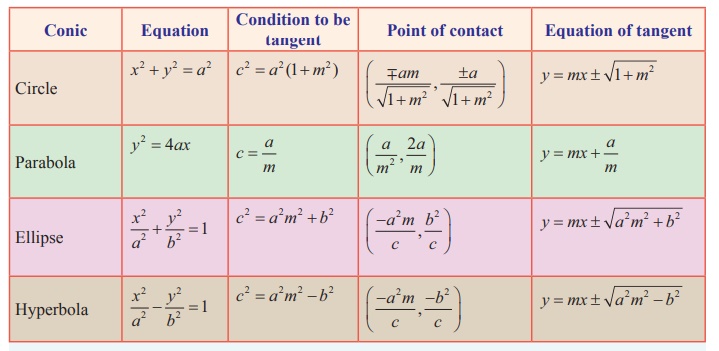
Table 3

Parametric forms

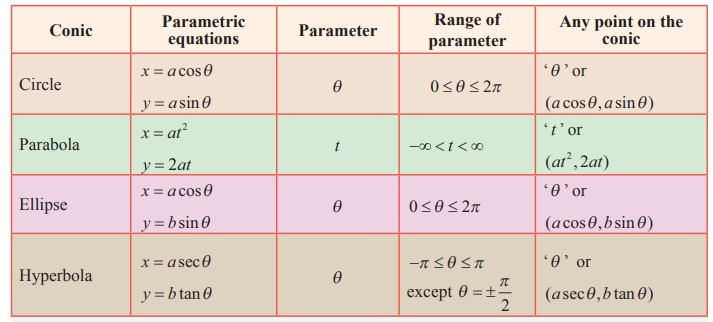
Identifying the conic from the general equation of conic Ax² + Bxy + Cy² + Dx + Ey + F = 0

The graph of the second degree equation is one of a circle, parabola, an ellipse, a hyperbola, a point, an empty set, a single line or a pair of lines. When,

(1) A = C = 1, B = 0, D = -2h, E = -2k, F = h² + k ² - r ²  the general equation reduces to (x - h)² + ( y - k )² = r² , which is a circle.

(2)      B = 0 and either A or C = 0 , the general equation yields a parabola under study, at this level.

(3)      A  ≠  C and A and C are of the same sign the general equation yields an ellipse.

(4)      A  ≠ C and A and C are of opposite signs the general equation yields a hyperbola

(5)      A = C and B = D = E = F = 0 , the general equation yields a point x² + y² = 0 .

(6)      A = C = F and B = D = E = 0 , the general equation yields an empty set x² + y² +1 = 0 , as there is no real solution.

(7)      A  ≠  0 or C ≠  0 and others are zeros, the general equation yield coordinate axes.

(8)      A = -C and rests are zero, the general equation yields a pair of lines x² - y² = 0 .