Parametric form of Conics

Parametric form of Conics

1. Parametric equations

Suppose f (t) and g(t) are functions of 't '. Then the equations x = f (t) and y = g(t) together describe a curve in the plane . In general 't ' is simply an arbitrary variable, called in this case a parameter, and this method of specifying a curve is known as parametric equations. One important interpretation of  't ' is time . In this interpretation, the equations x = f (t) and y = g(t) give the position of an object at time 't ' .

So a parametric equation simply has a third variable, expressing x and y in terms of that third variable as a parameter . A parameter does not always have to be 't ' . Using 't ' is more standard but one can use any other variable.

(i) Parametric form of the circle x² + y² = a²

Let P(x, y) be any point on the circle x² + y² = a².

Join OP and let it make an angle θ with x -axis.

Draw PM perpendicular to x -axis. From triangle OPM ,

x = OM = a cosθ

y = MP = a sinθ

Thus the coordinates of any point on the given circle are (a cos θ, a sin θ) and

x = a cosθ , y = a sinθ , 0 ≤ θ ≤ 2π are the parametric equations of the circle x² + y² = a².

Conversely, if x = a cosθ , y = a sinθ , 0 ≤ θ ≤ 2π ,

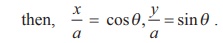
Squaring and adding, we get,

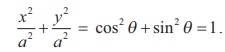
Thus x² + y²  = a² yields the equation to circle with centre (0, 0) and radius a units.

Note

(1) x = a cos t, y = a sin t , 0 ≤ t ≤ 2π also represents the same parametric equations of circle x² + y² = a² , 

t increasing in anticlockwise direction.

(2) x = a sin t, y = a cos t, 0 ≤ t ≤ 2π also represents the same parametric equations of circle x² + y² = a²,

t increasing in clockwise direction.

(ii) Parametric form of the parabola y² = 4ax

Let P(x₁ , y₁) be a point on the parabola

y₁² = 4ax₁

Parametric form of y² = 4ax is x = at², y = 2at, −∞ < t < ∞ .

Conversely if x = at² and y = 2at, −∞< t < ∞ , then eliminating 't ' between these equations we get y² = 4ax .

(iii) Parametric form of the Ellipse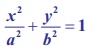 

Let P be any point on the ellipse. Let the ordinate MP meet the auxiliary circle at Q .

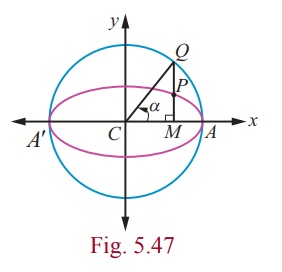
Let ∠ ACQ = α

∴  CM  = a cosα , MQ = a sin α

and Q(a cosα , a sin α )

Now x -coordinate of P is a cosα . If its y -coordinate is y′, then P(a cosα , y′) lies on

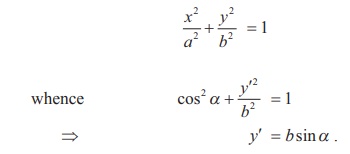
Hence P is (a cosα , b sin α ) .

The parameter α is called the eccentric angle of the point P . Note that α is the angle which the line CQ makes with the x -axis and not the angle which the line CP makes with it.

Hence the parametric equation of an ellipse is x = a cosθ , y = b sinθ , where θ is the parameter 0 ≤ θ ≤ 2π .

(iv) Parametric form of the Hyperbola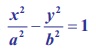 

Similarly, parametric equation of a hyperbola can be derived as x = a secθ , y = b tanθ , where θ  is the parameter.  −π  ≤ θ ≤ π except θ = ± π/2.

In nutshell the parametric equations of the circle, parabola,ellipse and hyperbola are given in the following table.

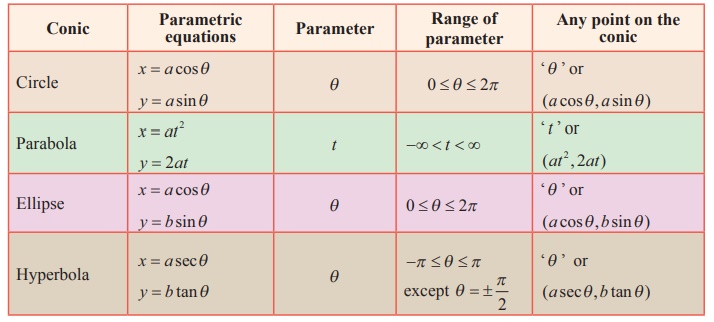
Remark

(1) Parametric form represents a family of points on the conic which is the role of a parameter. Further parameter plays the role of a constant and a variable, while cartesian form represents the locus of a point describing the conic. Parameterisation denotes the orientation of the curve.

(2) A parametric representation need not be unique.

(3) Note that using parameterisation reduces the number of variables at least by one.