Equation of a circle in standard form

Equation of a circle in standard form

(i) Equation of circle with centre (0, 0) and radius r

Let the centre be C(0, 0) and radius be r and P(x, y) be the moving point.

Note that the point P having coordinates (x, y) is represented as P(x, y) .

Then, CP  =  r and so CP² = r²

Therfore (x − 0)² + ( y − 0)² = r²

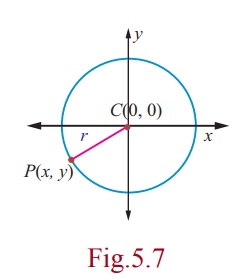
That is x² + y² = r²

This is the equation of the circle with centre (0, 0) and radius r 

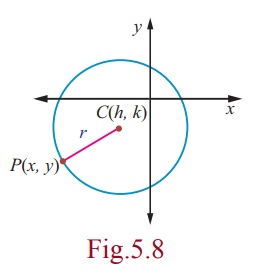
(ii) Equation of circle with centre (h, k) and radius r

Let the centre be C(h, k ) and r be the radius and P(x, y) be the moving point,

Then, CP = r and so CP² = r² .

That is, (x − h)² + ( y − k )² = r² .This is the equation of the circle in Standard form, which is also known as centre-radius form.

Expanding the equation, we get

x² + y² − 2hx − 2ky + h² + k² − r² = 0 .

Taking 2g = −2h, 2 f = −2k, c = h² + k² − r² , the equation takes the form

x² + y² + 2gx + 2 fy + c = 0 , called the general form of a circle.

The equation x² + y² + 2gx + 2 fy + c = 0 is a second degree equation in x and y possessing the following characteristics:

(i) It is a second degree equation in x and y ,

(ii) coefficient of x² = coefficient of y² ≠ 0 ,

(iii) coefficient of xy = 0 .

Conversely, we prove that an equation possessing these three characteristics, always represents a circle. Let 

ax²  + ay²  + 2g′x + 2 f y′  + c = 0 ………………………………(1)

be a second degree equation in x and y having characteristics (i), (ii) and (iii), a ≠ 0 . Dividing (1) by a, gives

equation (2) becomes x² + y² + 2gx + 2 fy + c = 0 .

Adding and subtracting g² and f² , we get x² + 2gx + g² + y² + 2 fy + f ² - g² - f ² + c = 0

⇒ (x + g)² + ( y + f )² = g ² + f ² – c

⇒ (x - (-g))²  + ( y - (- f ))²  = ( √[ g²  +  f ²  - c] )²

This is in the standard form of a circle with centre C (-g, - f ) and radius r = √[ g²  +  f ²  - c]. Hence equation (1) represents a circle with centre (-g, - f ) = ( -g’/a , - f’/a ) and radius

Note

The equation x² + y² + 2gx + 2 fy + c = 0 represents a circle with centre (–g, –f ) and radiu √[ g²  +  f ²  - c].

(i) It is a real circle if g² + f² - c > 0 ;

(ii) a point circle if g² + f ² - c = 0 ;

(iii) or an imaginary circle if g² + f ² - c < 0 with no locus.

Example 5.1

Find the general equation of a circle with centre (−3, −4) and radius 3 units.

Solution

Equation of the circle in standard form is  ( x - h)²  + ( y - k )²  = r ²

⇒   (x - (-3))²  + ( y - (-4))²  = 3²

⇒   ( x + 3)²  + ( y + 4)²  = 32

⇒ x² + y² + 6x + 8 y +16 = 0 .

Theorem 5.1

The circle passing through the points of intersection (real or imaginary) of the line lx + my + n = 0 and the circle x² + y² + 2gx + 2 fy + c = 0 is the circle of the form

x² + y² + 2gx + 2 fy + c + λ (lx + my + n) = 0 , λ ∈ R¹.

Proof

Let the circle be S : x2 + y2 + 2gx + 2 fy +  = 0 , … (1)

and the line be L : lx + my + n = 0 . … (2)

Consider  S + λL = 0  .  That is  x²  + y²  + 2gx + 2fy + c +λ(lx + my + n) = 0    ... (3)

Grouping the terms of x, y and constants, we get

 x²  + y²  + x(2g +λl)+ y(2f +λm)+ c +λn = 0 which is a second degree equation in x and y with coefficients of x² and y² equal and there is no xy term.

If (α, β) is a point of intersection of S and L satisfying equation (1) and (2), then it satisfies equation (3).

Hence  S + λL = 0  represents the required circle.

Example 5.2

Find the equation of the circle described on the chord 3x + y + 5 = 0 of the circle x² + y² = 16 as diameter.

Solution

Equation of the circle passing through the points of intersection of the chord and circle by Theorem 5.1 is x² + y² -16 + l (3x + y + 5) = 0 .

The chord 3x + y + 5 = 0 is a diameter of this circle if the centre 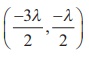 lies on the chord.

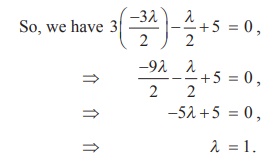
Therefore, the equation of the required circle is x² + y² + 3x + y -11 = 0.

Example 5.3

Determine whether x + y −1 = 0 is the equation of a diameter of the circle x² + y² − 6x + 4 y + c = 0 for all possible values of c .

Solution

Centre of the circle is (3, -2) which lies on x + y -1 = 0 . So the line x + y -1 = 0 passes through the centre and therefore the line x + y -1 = 0 is a diameter of the circle for all possible values of c .

Theorem 5.2

The equation of a circle with (x₁ , y₁ ) and (x₂ , y₂ ) as extremities of one of the diameters of the circle is (x − x₁ )(x − x₂ ) + ( y − y₁)( y − y₂) = 0.

Proof

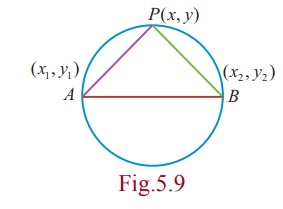
Let A(x₁ , y₁ ) and B(x₂ , y₂ ) be the two extremities of the diameter AB , and P(x, y) be any point on the circle. Then ÐAPB = π/2 (angle in a semi-circle).

Therefore, the product of slopes of AP and PB is equal to -1.

That is, 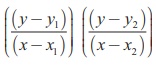 = −1 yielding the equation of the required circle as

 (x - x₁ )(x - x₂ ) + ( y - y₁ )( y - y₂ ) = 0 .

Example 5.4

Find the general equation of the circle whose diameter is the line segment joining the points (−4, −2) and (1,1) .

Solution

Equation of the circle with end points of the diameter as( x₁ , y₁ ) and ( x₂ , y₂ ) given in 

theorem 5.2 is 

( x - x₁ )( x - x₂ ) + ( y - y₁ )( y - y₂ ) = 0

⇒  ( x + 4)( x -1) + ( y + 2)( y -1) = 0

⇒ x² + y² + 3x + y - 6 = 0 which is the required equation of the circle.

Theorem 5.3

The position of a point P(x₁ , y₁ ) with respect to a given circle x² + y² + 2gx + 2 fy + c = 0 in the Plane containing the circle is Outside or on or inside the circle according as x² + y² + 2gx + 2 fy + c is

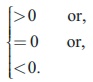
Proof

Equation of the circle is x² + y² + 2gx + 2 fy + c = 0 with centre C (-g, - f ) and radius r =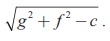 

Let P(x₁, y₁ ) be a point in the plane. Join CP and let it meet the circle at Q .Then the point P is outside, on or within the circle according as

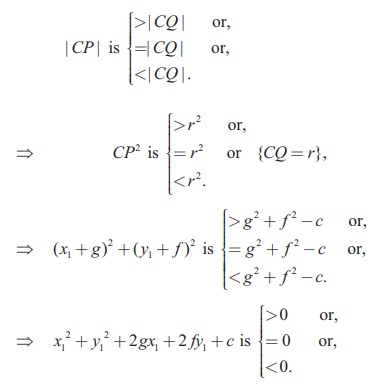
Example 5.5

Examine the position of the point (2, 3) with respect to the circle x² + y² − 6x − 8 y +12 = 0.

Solution

Taking (x₁, y₁) as (2, 3), we get 

x² + y² + 2gx₁ + 2 fy₁ + c = 2² + 3² - 6 ´ 2 - 8´ 3 +12 ,

= 4 + 9 -12 - 24 + 12 = -11 < 0.

Therefore, the point (2, 3) lies inside the circle, by theorem 5.3.

Example 5.6

The line 3x + 4 y −12 = 0 meets the coordinate axes at A and B . Find the equation of the circle drawn on AB as diameter.

Solution

Writing the line 3x + 4y = 12, in intercept form yields x/4 + y/3 = 1. Hence the points A and B are (4, 0) and(0, 3) .

Equation of the circle in diameter form is 

( x - x₁ )( x - x₂ ) + ( y - y₁ )( y - y₂ ) = 0

( x - 4)( x - 0) + ( y - 0)( y - 3) = 0

x² + y² - 4x - 3y = 0

Example 5.7

A line 3x + 4 y +10 = 0 cuts a chord of length 6 units on a circle with centre of the circle (2,1) . Find the equation of the circle in general form.

Solution

C(2,1) is the centre and 3x + 4 y +10 = 0 cuts a chord AB on the circle. Let M be the midpoint of AB . Then we have

AM  = BM = 3 . Now  BMC is a right triangle.

So, we have CM  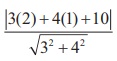=  = 4.

By Pythogoras theorem BC² = BM² + MC²  = 3² + 4² = 25

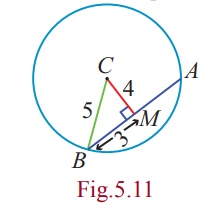
BC = 5 = radius.

So, the equation of the required circle is (x - 2)² + ( y -1) = 5²

x² + y² - 4x - 2 y – 20 = 0.

Example 5.8

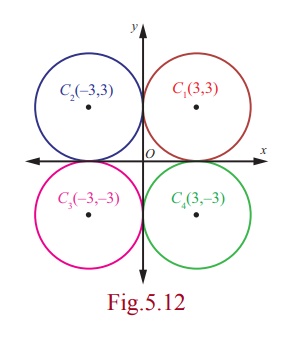
A circle of radius 3 units touches both the axes. Find the equations of all possible circles formed in the general form.

Solution

As the circle touches both the axes, the distance of the centre from  both the axes is 3 units, centre can be (±3, ±3) and hence there are four circles with radius 3, and the required equations of the four circles are x² + y² ± 6x ± 6 y + 9 = 0 .

Example 5.9

Find the centre and radius of the circle 3x² + (a +1) y² + 6x - 9y + a + 4 = 0.

Solution

Coefficient of x² = Coefficient of y² (characteristic (ii) for a second degree equation to represent a circle).

That is, 3 = a +1 and a = 2 .

Therefore, the equation of the circle is 

3x² + 3y² + 6x - 9 y + 6 = 0

x² + y² + 2x - 3y + 2 = 0

So, centre is ( -1, 3/2 ) and radius r =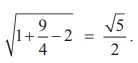 

Example 5.10

Find the equation of the circle passing through the points (1,1), (2, −1) , and (3, 2) .

Solution

Let the general equation of the circle be

x² + y² + 2gx + 2 fy + c = 0        ……….(1)

It passes through points (1,1), (2, -1) and (3, 2) .

Therefore, 2g + 2 f + c = -2 , … (2)

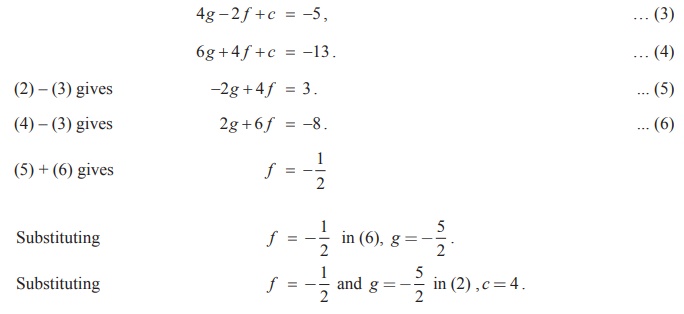
Therefore, the required equation of the circle is

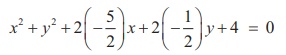
Þ x² + y² - 5x - y + 4 = 0

Note

Three points on a circle determine the equation to the circle uniquely. Conversely three equidistant points from a centre point forms a circle.