Special theory of relativity

Special theory of relativity

It is a direct outcome of new realisations of the nature of mass, length and time. It discards the absolute motion through space and deals with objects or observers, that are moving with uniform velocities relative to each other.

The two fundamental postulates of the special theory of relativity are :

       i.            The laws of Physics are the same in all inertial frames of  reference.

     ii.            The velocity of light in free space is a constant in all the frames of reference.

1.Length contraction

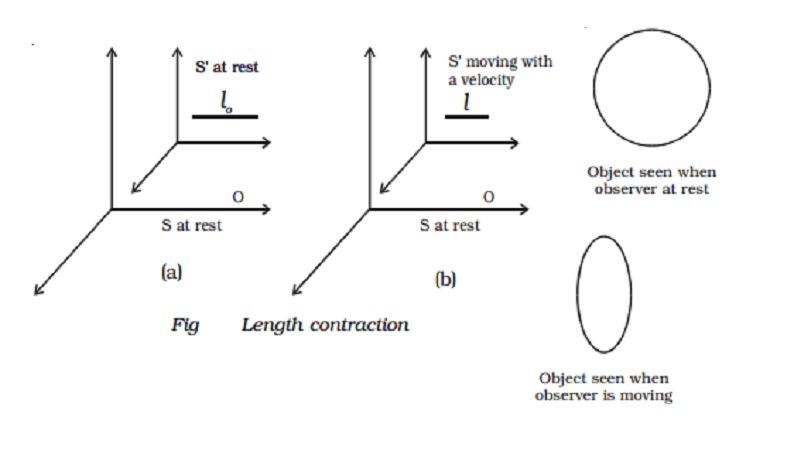
Consider two frames of references S and S′ to be initially at rest. A rod is placed in the frame of reference S′ and an observer O is in S (Fig ). The length of the rod in S′ as measured by the observer in S is l_o.

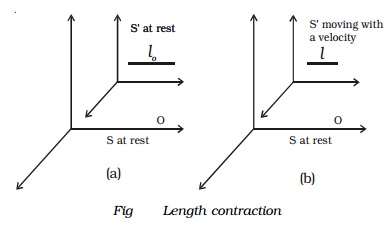
Now the frame of reference S′ moves with a velocity v along the positive X-axis. Now, the length of the rod is measured as l by the observer in S. Then

l = l_o rt(1-(v²/c²))

l<l₀

Thus the length of the rod moving with a velocity v relative to the observer at rest is contracted by a factor root(1-(v²/c²)) in the direction of motion.  This  is  known as Lorentz - Fitzgerald contraction.

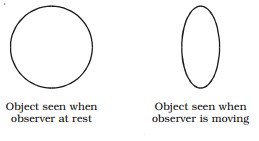
Example : A circular object will appear as an ellipse for a fast moving observer as shown in Fig.

Time dilation

Consider two frames S and S′. Let S′ be moving with a velocity v with respect to S in the positive X-direction. Suppose a clock situated in the frame S′ at a position gives out signals at an interval t_o.

If this interval is observed by an observer in frame S, then the interval t recorded by him is

t = t₀/root(1-(v²/c²))

i.e.  t>t₀

To  a stationary observer  in  S,  time  interval  appears  to  be lengthened by a factor   1/root(1-(v²/c²))  In otherwords, a moving clock appears to be slowed down to a stationary observer. This is known as time dilation.

Example : The clock in the moving space ships will appear to go slower than the clocks on the earth.

3 Variation of mass with velocity

According to Newtonian mechanics, the mass of a body does not change with velocity. But according to Einstein, the mass of the body changes with velocity. Einstein established the relation between the mass of a body at rest (m_o) and the mass of the same body moving with a velocity v is,

m = m₀/root(1-(v²/c²))

Example : Electrons accelerated in a particle accelerator, cyclotron with a very high velocity acquire increased mass, exactly as predicted by the above expression.