Chapter: 11th 12th std standard Class Physics sciense Higher secondary school College Notes
Satellites: Orbital velocity, Time period and Energy
Satellites
A body moving in an orbit around a
planet is called satellite. The moon is the natural satellite of the Earth. It
moves around the Earth once in 27.3 days in an approximate circular orbit of
radius 3.85 × 105 km. The first artificial satellite Sputnik was
launched in 1956. India launched its first satellite Aryabhatta on April 19,
1975.
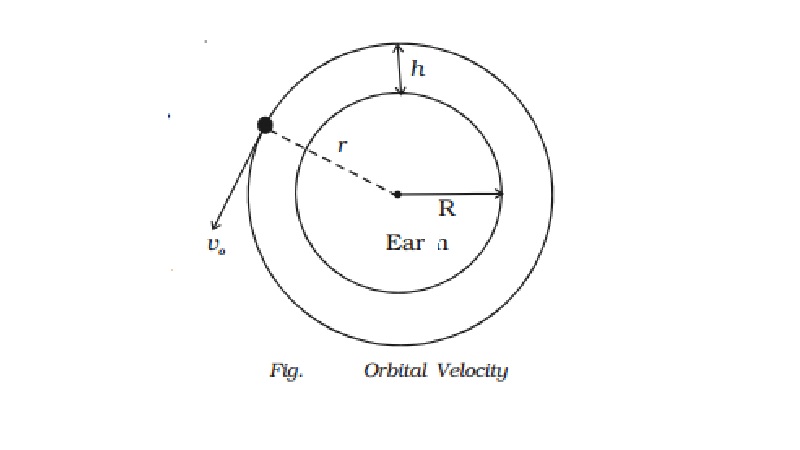
Orbital velocity
Artificial satellites are made to
revolve in an orbit at a height of few hundred kilometres. At this altitude,
the friction due to air is negligible. The satellite is carried by a rocket to
the desired height and released horizontally with a high velocity, so that it
remains moving in a nearly circular orbit.
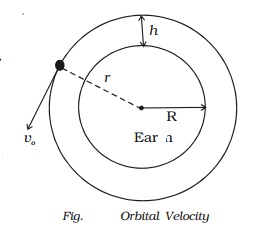
The horizontal velocity that has to be imparted to a
satellite at the determined height so that it makes a circular orbit around the
planet is called orbital velocity.
Let us assume that a satellite of
mass m moves around the Earth in a
circular orbit of radius r with
uniform speed vo. Let the
satellite be at a height h from the
surface of the Earth. Hence, r = R+h,
where R is the radius of the Earth.
The centripetal force required to
keep the satellite in circular orbit is F = mv02/r = mv02
/ R+h
The gravitational force between
the Earth and the satellite is
F = GMm / r2 =
GMm/(R+h)2
For the stable orbital motion,
v0 = root(gR2/R+h)
If the satellite is at a height
of few hundred kilometers (say 200 km), (R+h) could be replaced by R.
orbital velocity, vo = rt(gR)
If the horizontal velocity
(injection velocity) is not equal to the calculated value, then the orbit of
the satellite will not be circular. If the injection velocity is greater than
the calculated value but not greater than the escape speed (ve = 2 vo),
the satellite will move along an elliptical orbit. If the injection velocity
exceeds the escape speed, the satellite will not revolve around the Earth and
will escape into the space. If the injection velocity is less than the
calculated value, the satellite will fall back to the Earth.
Time period of a satellite
Time taken by the satellite to
complete one revolution round the Earth is called time period.
Time period, T = circumference
of the orbit / orbital velocity
T = 2πr / v0
= 2π(R +h) / v0
where r is the radius of the
orbit which is equal to (R+h).
v0 = root[GM/R+h] so
T = 2π (R+h) root[(G+h)/GM]
As GM = gR2, T = 2π root[(R+h)3/gR2]
If the satellite orbits very
close to the Earth, then h << R
T = 2π root[R/g]
Energy of an orbiting satellite
A satellite revolving in a
circular orbit round the Earth possesses both potential energy and kinetic
energy. If h is the height of the satellite above the Earth's surface and R is
the radius of the Earth, then the radius of the orbit of satellite is r = R+h.
If m is the mass of the
satellite, its potential energy is,
EP = - GMm/r
where M is the mass of the Earth.
The satellite moves with an orbital velocity of vo = root[GM/(R+h)]
Hence, its kinetic energy is,
EK = 1/2 mvo2
EK = GMm / 2(R+h)
The total energy of the satellite
is, E = EP + EK
E = − GMm / 2(R+h)
The negative value of the total
energy indicates that the satellite is bound to the Earth.
Geo-stationary satellites
A
geo-stationary satellite is a particular type used in television and telephone
communications. A number of communication
satellites which appear to remain in fixed
positions at a specified height above the equator are called synchronous
satellites or geo-stationary satellites. Some television programmes or events occuring in other countries are
often transmitted 'live' with the help of these satellites.
For a satellite
to appear fixed at a position above a certain place on the Earth, its orbital
period around the Earth must be exactly equal to the rotational period of the
Earth about its axis.
Consider a
satellite of mass m moving in a
circular orbit around the Earth at a distance r from the centre of the Earth. For synchronisation, its period of
revolution around the Earth must be equal to the period of rotation of the
Earth (ie) 1 day = 24 hr = 86400 seconds.
The speed of the satellite in its
orbit is
v = Circumference
of orbit / Time period
v = 2π r / T
The centripetal force is F = mv2/r
F = 4mπ2r /T2
The gravitational force on the
satellite due to the Earth is
F = GMm/r2
For the stable orbital motion 4mπ2r
/ T2 = GMm / r2
We know that, g = GM/R2
r3 = gR2T2
/ 4 π2
The orbital radius of the geo-
stationary satellite is, r = [gR2T2 / 4 π2]1/3
Substituting T = 86400 s, R = 6400 km
and g = 9.8 m/s2, the
radius of the orbit of geo-stationary satellite is calculated as 42400 km.
The height of the geo-stationary
satellite above the surface of the Earth is h
= r - R = 36000 km.
If a satellite is parked at this
height, it appears to be stationary. Three satellites spaced at 120o
intervals each above Atlantic, Pacific and Indian oceans provide a worldwide
communication network.
Polar satellites
The polar satellites revolve
around the Earth in a north−south orbit passing over the
poles as the Earth spins about its north - south axis.
The polar satellites positioned
nearly 500 to 800 km above the Earth travels pole to pole in 102 minutes. The
polar orbit remains fixed in space as the Earth rotates inside the orbit. As a
result, most of the earth's surface crosses the satellite in a polar orbit.
Excellent coverage of the Earth is possible with this polar orbit. The polar
satellites are used for mapping and surveying.
Uses of satellites
(i) Satellite communication
Communication satellites are used
to send radio, television and telephone signals over long distances. These
satellites are fitted with devices which can receive signals from an Earth -
station and transmit them in different directions.
(ii) Weather monitoring
Weather satellites are used to
photograph clouds from space and measure the amount of heat reradiated from the
Earth. With this information scientists can make better forecasts about
weather. You might have seen the aerial
picture of our country taken by the satellites, which is shown daily in the
news bulletin on the television and in the news papers.
(iii) Remote sensing
Collecting of information about
an object without physical contact with the object is known as remote sensing.
Data collected by the remote sensing satellities can be used in agriculture,
forestry, drought assessment, estimation of crop yields, detection of potential
fishing zones, mapping and surveying.
(iv) Navigation satellites
These satellites help navigators
to guide their ships or planes in all kinds of weather.
Related Topics