Rutherford's α - particle scattering experiment

Rutherford's α - particle scattering experiment

Rutherford and his associates studied the scattering of the α - particles by a thin gold foil in order to investigate the structure of the atom. An α-particle is a positively charged particle having a mass equal to that of helium atom and positive charge in magnitude equal to twice the charge of an electron. They are emitted by many radioactive elements. The scattering of α-particles provide useful information about the structure of the atom.

Experimental arrangement

A fine pencil of α−particles was obtained from a radioactive material like radium or radon by placing it in a lead box with narrow opening as shown in Fig.

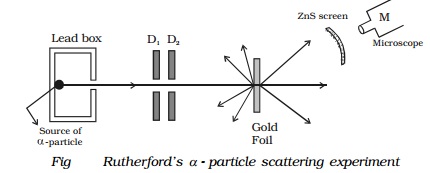
The α-particles are emitted from the source in all possible directions, but only a narrow beam emerges from the lead box. The remaining α-particles are absorbed in the lead box itself. After passing through the diaphragms D₁ and D₂, a narrow beam of α-particles incident on a thin gold foil, are scattered through different angles. The scattered α-particles strike a fluorescent screen coated with zinc sulphide. When the α-particles strike the screen, tiny flashes of light are produced. The observations can be made with the help of a low power microscope.

Observations and conclusions

(i)  Most  of  the  α particles    either passed straight through the gold foil or were scattered by only  small  angles  of  the order  of  a  few  degrees.

This observation led to the conclusion       that an atom has a lot of empty space as shown in Fig.

(ii) A few α particles were scattered in the backward direction, which led Rutherford to conclude that the whole of the positive charge was concentrated in a tiny space of about 10^-14m. This region of the atom was named as nucleus. Only a small number of particles approaches the nucleus of the atom and they were deflected at large angles.

Distance of closest approach

An α particle directed towards the centre of the nucleus will move close upto a distance r_o as shown in Fig, where its kinetic energy will appear as electrostatic potential energy. After this, the α particle begins to retrace its path. This distance r_o is known as the distance of the closest approach.

Let m and v be the mass and velocity of the α particle directed towards the centre of the nucleus. Then, the kinetic energy of the particle,

E_k = ½ mv₂                     …………… (1)

Since, charge of an α-particle is 2e and that of the nucleus of the atom is Ze, the electrostatic potential energy of the α particle, when at a distance r_o from the centre of the nucleus is given by,

E_p = ( 1/ 4πε₀ ) . (2e )( Ze) / r₀        ............(2)

where Z is the atomic number of the atom and ε_o, the permittivity of free space.

On reaching the distance of the closest approach r_o, the kinetic energy of the α particle appears as its potential energy.

E_p = E_k

 ( 1/ 4πε₀ ) . (2e )( Ze) / r₀   = ½ mv₂ 

r₀ = ( 1/ 4πε₀ ) 4Ze² / mv²