Chapter: 11th 12th std standard Class Physics sciense Higher secondary school College Notes
Rotational motion of rigid bodies

Rotational motion of rigid bodies
Rigid body
A rigid body is defined as that body which does not undergo any change in shape or volume when external forces are applied on it. When forces are applied on a rigid body, the distance between any two particles of the body will remain unchanged, however, large the forces may be.
Actually, no body is perfectly rigid. Every body can be deformed more or less by the application of the external force. The solids, in which the changes produced by external forces are negligibly small, are usually considered as rigid body.
Rotational motion
When a body rotates about a fixed axis, its motion is known as rotatory motion. A rigid body is said to have pure rotational motion, if every particle of the body moves in a circle, the centre of which lies on a straight line called the axis of rotation (Fig.). The axis of rotation may lie inside the body or even outside the body. The particles lying on the axis of rotation remains stationary.
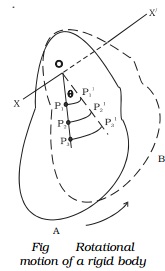
The position of particles moving in a circular path is conveniently described in terms of a radius vector r and its angular displacementθ . Let us consider a rigid body that rotates about a fixed axis XOX′ passing through O and perpendicular to the plane of the paper as shown in Fig. Let the body rotate from the position A to the position B. The different particles at P1,P2,P3. ,... in the rigid body covers unequal distances P1P1′, P2P2′, P3P3′,... in the same interval of time. Thus their linear velocities are different. But in the same time interval, they all rotate through the same angle θ and hence the angular velocity is the same for the all the particles of the rigid body. Thus, in the case of rotational motion, different constituent particles have different linear velocities but all of them have the same angular velocity.
Equations of rotational motion
As in linear motion, for a body having uniform angular acceleration, we shall derive the equations of motion.
Let us consider a particle start rotating with angular velocity ω0 and angular acceleration α. At any instant t, let ω be the angular velocity of the particle and θ be the angular displacement produced by the particle.
Therefore change in angular velocity in time t = ω - ω0
But, angular acceleration = change in angular velocity/ time taken
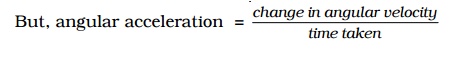
α= ω - ωο / t
ω = ωο + αt
The average angular velocity = (ω+ ωο / 2 )
The total angular displacement = average angular velocity x time taken

Equations (2), (4) and (6) are the equations of rotational motion.
Related Topics