Response spectrum characteristics

Response spectrum characteristics

Let u˙˙_{g 0} , u˙ _{g 0} , u_{g 0} be the peak values of ground acceleration, velocity and displacement respectively. Response spectrum values are presented to normalized form in Fig. 17.22. The period range may be separated by period values at a, b, c, d, e and f where T_a = 0.033 s, T_b = 0.125 s, T_e = 10 s, T_f = 33 s.

We identify the effects of damping on systems with short period T_n < T_a = 0.033, the peak-pseudo acceleration A = S_pa approaches u˙˙_{g 0} and D = Sd is very small. For a fixed mass, very short period means extremely stiff or essentially rigid. Deformation will be very small and it moves with the ground.

For a system with longer period S_d with approach to u_g0, S_pa is very small. For a rigid mass the structure is flexible. In that case

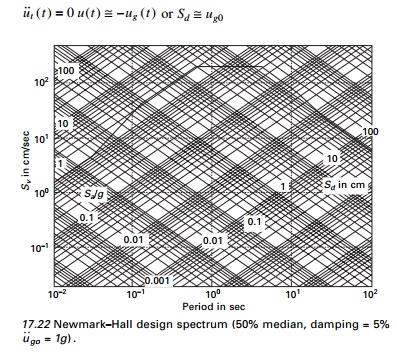
For short period system T_nT_a < T_n < T_c. S_pa exceeds u˙˙_{g 0} with amplification depending on T_n, ρ over a period range T_b to T_c, S_pa may be constant = u˙˙_{g 0} × amplification factor depending on ρ .

For a long period T_d < T_n < T_f, S_d generally exceeds u_g0 with amplification generally depending on ρ. Over a portion of the period T_d to T_e(3–10 s) S_d may be idealized as a constant × amplification factor depending on ρ. For intermediate period systems with T_n between T_c < T_n < T_d, S_pv exceeds u˙_{g 0} Over the period range S_pv may be idealized as a constant value × amplification factor depending on ρ.

Based on the observation of response spectrum, it is logical to divide the spectrum into three ranges:

•       Long period range T_n > T_d. Displacement-sensitive region because structure response is related mostly to ground displacement.

•       Short period range T_n < T_c. Acceleration-sensitive region because structural response is mostly related to ground acceleration.

•       Intermediate range T_c < T_n < T_d. Velocity-sensitive region because structural response appears to be better related to ground velocity than to other ground motion parameters.

The periods T_a, T_b, T_e, T_f on the idealized spectrum are independent of damping but T_c and T_d vary with damping.

Idealizing a spectrum by a series of straight lines a, b, c, d, e, f in the four-way logarithmic plot is obviously not a precise process. The period values at a–f and amplification factors are judgemental. The advantages of an idealized spectrum are that we can very easily construct a design spectrum. These values vary from one ground motion with others.

Example 17.7

Consider an elastic design spectrum, 84.1% for ground motion u˙˙_{g 0} = 1 g ; u˙_{g 0} = 121.92 cm/s; u_g0 = 91.44 cm; ρ = 5%. Using the program developed it is possible to construct a design spectrum as shown in Fig. 17.23.

Solution

From Fig. 17.23, we can construct a pseudo-acceleration spectrum in terms of g plotted in log scale in Fig. 17.24 for ground acceleration of 1g and damping factor 5%. Similarly for various values of ρ an elastic pseudo-acceleration spectrum can be plotted in log scale as shown in Fig. 17.25 and a design spectrum in Fig. 17.26. If pseudo-acceleration is plotted at a normal scale, the diagram is as shown in Fig. 17.26.

Example 17.8

Estimate the maximum sensitive response for the industrial building of Example 17.1 using Newmark–Hall design spectra for an anticipated ground acceleration

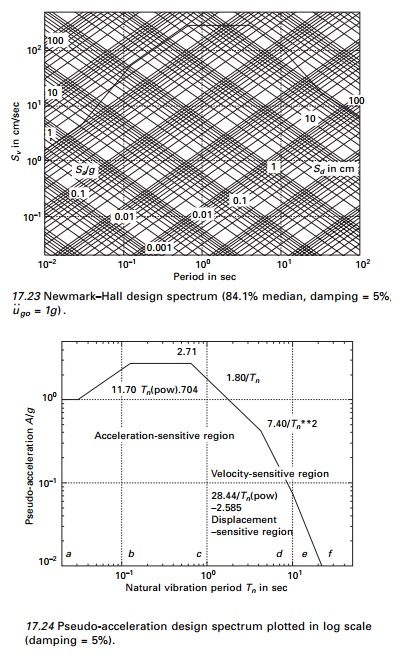
of 0.308g and for a damping factor of 0.05. Compare the results with the maximum response obtained from time history analysis.

Solution

Damping = 5%

(i)    NS direction, T = 0.567 s

From chart (see Fig. 17.23), spectra value S_d = 6.35 cm; S_pv = 71.12 cm/s; S_pa = 784.35 cm/s².

Maximum base shear = mS_pa

= 131 697.2 × 7.843

1032.9 kN

(ii)             EW direction S_d = 20 mm

S_pv = 393.7 mm/s S_pa = 7.843 mm/s² ω_n = 20 rad/s

T = 0.313

Maximum base shear = mS_pa

= 1032.9 kN

Comparison of the maximum response obtained from time history analysis response spectra and design spectrum analysis is presented in Table 17.4 for NS direction. There is a considerable discrepancy between the results of response spectrum and design spectrum. The former represents the response to a specific earthquake while the latter represents predicted response to any earthquake.