Earthquake intensity and magnitude

Earthquake intensity and magnitude 

1  Intensity

The oldest useful yardstick of the strength of an earthquake is the earthquake intensity. The intensity of an earthquake is used to determine its severity at a particular location as determined by human reactions to Earth’s movement, observed damage to structures, and observation of other physical effects. Because earthquake intensity assessments do not depend on instruments, but on the actual observation of effects in the seismal zone, intensities can be assigned to historical earthquakes. In this way the historical record becomes of utmost importance in modern estimates of seismological risk. Thus the intensity will vary with distance from the causative fault and with local ground conditions. Intensity is a qualitative measure of the actual shaking at a location during an earthquake, and assigned as Roman capital numerals.

The first intensity scale was developed by de Rossi of Italy and Forel of Switzerland in the 1880s. This scale, with values I to X, was used for reports of the intensity of the 1906 San Francisco earthquakes, for example. A new refined scale was devised by the Italian volcanologist and seismologist Mercalli in 1902 with a 12-degree range from I to XII. More refined scales were developed by Cancanio. In 1931 Frank Neumann and H O Wood proposed a 12 grade modified Mircalli (MMI) scale, which has been widely adopted in South America, and other parts of the world. Other intensity scales in use today are the 12-grade Medvedev â€' Sponheuer Karnik (MSK-64) scale and the 8-grade Japanese Meteorological Agency (JMA) scale. Because intensity scales are subjective and highly dependent on the construction practices and socio-economic conditions of a country, and bear no specific relation to the ground motion, correlation among the various intensity scales is not easily done. Both the MMI and the MSK scales are quite similar and range from I (least perceptive) to XII (most severe). The intensity scales are based on three features of shaking:

•         perception by people and animals;

•         performance of buildings;

changes to natural surroundings.

IS1893 (Part 1): 2002 adopts a comprehensive intensity scale (MSK-64) and this is given in Table 16.5 for completeness.

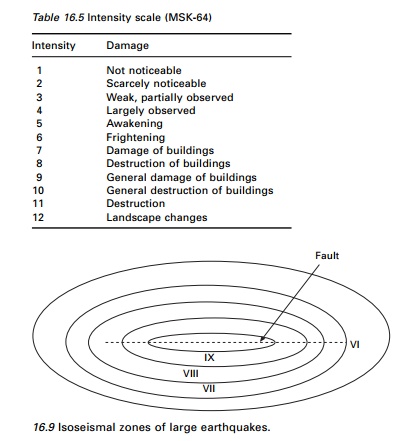
The intensity of the earthquake is greatest in the vicinity of the causative fault and decreases with distance from the fault. Curves of equal intensity as shown in Fig. 16.9 called ‘isoseismals’ assume a bell-shaped pattern for small earthquakes. For large earthquakes having a slipped length of fault of several hundred kilometres, the idealized isoseismals become quite elongated in a direction parallel to causative fault. In actuality, however, the isoseismals are more complex as they are influenced by such factors as local site and geological conditions.

2  Earthquake magnitude

If sizes of earthquakes are to be compared worldwide, a measure is needed that does not depend, as does intensity, on the density of population and type of construction. A strictly quantitative scale that can be applied to earthquakes

in both inhabited and uninhabited regions was originated by Wadati in 1931 in Japan and developed by Charles Richter in 1935 in California.

Richter defined the magnitude of a local earthquake as the logarithm to base ten of the maximum seismic wave amplitude in micrometres (10^â€'4 cm) recorded on a Wood Anderson seismograph located at a distance of 100 km from the earthquake epicentre. This means that a ten-fold increase in the amplitude of the earthquake waves results in the magnitude of the scale going up by one unit.

Since the fundamental period of a seismograph is 0.8 s, it selectively amplifies those seismic waves with a period ranging from 0.5 to 1.5 s because the natural period of many buildings is within this range. The local Richter magnitude remains the value familiar to engineers. Richter also found that among earthquakes occurring at the same distance, larger earthquakes have bigger wave amplitude than smaller earthquakes and also greater distances have lower amplitude than at shorter distances. This is obtained from the seismogram and accounts for the dependence of wave-form amplitude and epicentral distance. This scale is called Richter scale or local magnitude scale.

The magnitude of the earthquake is determined from the expression:

M = log₁₀ A                   ---- --- - 16.4

where A is the maximum seismic amplitude in (10^â€'4 m). However, a standard seismograph is not always set at a distance of 100 km from the epicentre, in which case it can be modified as

M = log₁₀ A â€' log₁₀ A_{0           --- -- - -} 16.5

where A is the maximum seismic wave amplitude for the measured earthquake at a given epicentre distance and A₀ is the seismographic reading produced by standard earthquake (A₀ = 0.001). A correlation between the amount of energy E_f released at the causative fault and the Richter magnitude was developed by Gutenberg and Richter and is expressed as

log₁₀ E_f = 4.8 + 1.5M                    --- --- 16.6

Because the Richter magnitude is a logarithmic scale, an increase of unity in magnitude represents 10-fold increase in the amplitude of the seismic waves (e.g., a reading of 7 represents 10 times greater amplitude than a reading of 6).

For instance, energy release for earthquakes of values 6 and 7.

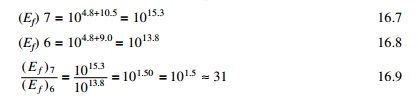
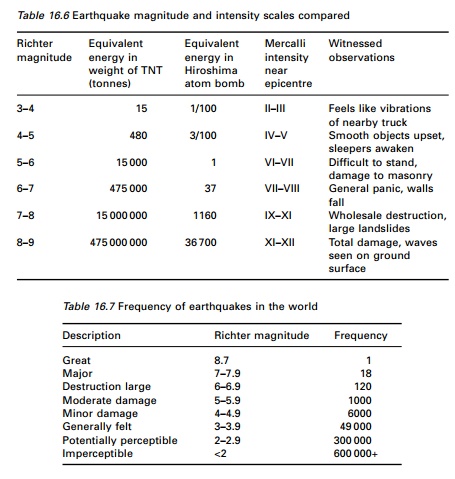
So the energy released in an M7 earthquake is about 31 times that released in an M6 and in an M8 the energy released is about 1000 (31 ïƒ- 31) times that released in an M6 earthquake. Most of the energy released goes into heat and fracturing rocks and only a small fraction of it (fortunately) goes into the seismic waves that travel a larger distance, causing shaking of the ground en route and hence damage to structures. The energy releases for various magnitudes of earthquake and the corresponding intensity scales are compared in Table 16.6.

An empirical relation between Richter magnitude M, modified Mercalli intensity (MM) and focal distance ‘d’ in km was suggested by Esteva and Rosenblueth as

MM = 8.16 + 1.45 Mâ€'2.46 ln (d)           --- --- 16.10

It is interesting to note that energy released in an M6.3 earthquake is equivalent to that released by the 1945 atom bomb dropped on Hiroshima.

Earthquakes having M < 5 generate ground motions unlikely to cause damage because of their very short duration and moderate acceleration. An earthquake with a magnitude of 7.2 would be considered a strong earthquake. Earthquakes with magnitudes above 7.5 are referred to as great earthquakes, whereas earthquakes with magnitude < 2 or less are known as micro-earthquakes. Table 16.7 shows the frequency of occurrence of various types of earthquakes. There are one million earthquakes annually, 80 000/month;

2600/day; 2/minute; 1 earthquake is felt every 30 s. The frequency of earthquake for any magnitude >M is given by N = 10^{6.7â€'0.9M}.

At its inception, the idea behind the Richter-local magnitude scale (ML) was a modest one, applicable to shallow earthquakes and epicentre distance

< 600 km. Today the method has been extended to a number of types of seismographs throughout the world. Consequently there are a variety of magnitude scales on different formulae for epicentre distance and the ways of choosing appropriate wave amplitude.

3  Surface wave magnitude (M_s)

Periods of 20 s are usually dominant on seismograph records of distant earthquakes (epicentral distance > 2000 km). Gutenberg defined a magnitude scale based on measuring the amplitude of surface waves within a period of 20 s.

4  Body wave magnitude (M_b)

Deep focus earthquakes have only small or insignificant trains of surface waves. It is customary to measure the velocity of the P wave, which is not affected by focal depth of the source.

5  Moment magnitude (M_w)

The best estimates of an earthquake’s magnitude, especially for great earthquakes, are given by the moment magnitude (M_w). This scale emulates the magnitude of an earthquake in terms of seismic movement, M₀, that is directly related to the amount of energy released in the earthquake. M_w is expressed as

M_w = log₁₀ (M₀/1.5) â€' 10.7                            ----16.11

where M₀ = Î¼ A_sD, Î¼ = parameter characterizing the rigidity of the material surrounding the causative fault, A_s = slipping area and D = distance of slip.

In the light of the above discussions, an application of different scales has been suggested for measuring shallow earthquakes of various magnitudes.

M_D for magnitudes < 3           --- --- 16.12

M_L or M_b 3< M < 7           --- --- 16.13

M_s 5 < M < 7.5           --- --- 16.14

M_w for all magnitudes           --- --- 16.15

Table 16.8 shows some of the major earthquakes in the world 1971â€'2008. Out of various earthquakes occurring in the world, the circum-pacific seismic zone is the principal zone which accounts for 80% of all earthquakes

and most tectonic activity. At some places chains of volcanoes cause a ‘circle of fire’; Alpide zone accounts for 15% of earthquakes and the remaining are in the narrow zone of Atlantic and Indian Ocean.