Chapter: Civil : Structural dynamics of earthquake engineering
Introduction to Dynamics
Introduction
to dynamics
Key words: periodic
motion, stochastic, natural frequency, finite element method, resonance.
Introduction
This text is concerned with the
analysis of structures subjected to dynamic loads. Dynamics in this context
means time varying. Both application of load and removal of load necessarily
vary with time. Hence, the internal stresses and the resulting deflections are
also time dependent or dynamic in nature.
In the real world, no loads that
are applied to a structure are truly static. All bodies possessing mass and
elasticity are capable of vibration. Thus most engineering machines and
structures experience vibration to some degree and their design generally
requires consideration of oscillatory behaviour.
The effects of vibration are very
common in our daily life. We live on the beating of our hearts. Planetary
motion is also another example of vibration. These motions are called periodic
motions (periodic motion is a motion that repeats itself regularly after
a certain interval of time). This interval of time is known as the period
of the system or motion. In general, vibration has both good and bad effects.
In civil engineering, the good effect of vibration is harnessed by the
compaction of fresh concrete. The bad effects of vibrations on a structure are
those produced by natural forces such as wind gusts, and earthquakes and by
mechanical forces on a bridge.
Oscillatory systems can be
broadly characterized as linear or nonlinear. In general, for linear systems,
the principle of superposition is valid, and the mathematical techniques
available are well developed. Techniques for the analysis of nonlinear systems
are less well known and difficult to apply, since changes in stiffness and
damping characteristics occur during nonlinear inelastic response.
In general, vibration can be
classified as free vibration and forced vibration. Free vibration takes place
when a system oscillates under the actions of forces inherent in the system
itself and external forces are absent. The system under free vibration will
vibrate at one or more of its natural frequencies, which are properties of the
dynamics system.
Vibration that takes place under
the excitation of external forces is called forced vibration. If the frequency
of excitation coincides with one of the natural frequencies of the system, a
condition of resonance occurs, resulting in large oscillations in structures,
which ultimately results in the failure of the structure.
Different types of
dynamic loads
Dynamic loads may be classified
as Ã'deterministicÕ and Ã'non-deterministicÕ. If the magnitude,
point of application of the load and the variation of the load with respect to
time are known, the loading is said to be deterministic and the analysis of a
system to such loads is defined as deterministic analysis. On the other hand,
if the variation of load with respect to time is not known, the loading is
referred to as random or stochastic loading and the corresponding
analysis is termed as non-deterministic analysis.
Dynamic loads may also be
classified as periodic and non-periodic loadings. When a loading repeats itself
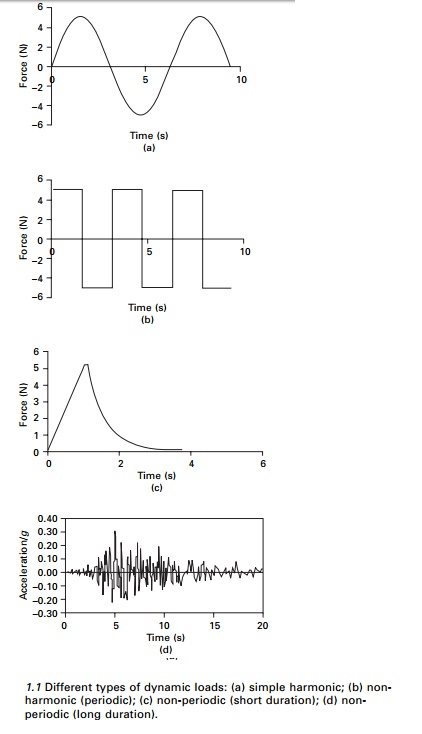
at equal time intervals then it is called periodic loading. A single form of
periodic loading is either a sine or cosine function as shown in Fig. 1.1a. A
vibration induced due to rotating mass is a periodic motion. This type of
periodic loading is called simple harmonic motion as shown in Fig. 1.1a. The
type of loading shown in Fig. 1.1b is a periodic loading but non-harmonic.
Later on we will see that most periodic loads can be represented by summing
sufficient number of harmonic terms in a Fourier series. Any loading which does
not come under the category of periodic loading is termed as non-periodic.
Blast loading shown in Fig. 1.1c and earthquake ground motion as shown in Fig.
1.1d are the examples of non-periodic loads.
Difference between
dynamic and static problems
In two aspects, a dynamic problem is different
from a static problem. The first and most obvious difference is the
time-varying load and the response is also time varying. This needs analysis
over a specific interval of time. Hence dynamic analysis is complex and
computationally extensive and expensive compared with static analysis. The
other difference between dynamic and static problems is the major occurrence of
inertia forces when the loading is dynamically applied. Consider a water tank
as shown in Fig. 1.2a subjected to load F at the top. The resulting
deflection, shear force and bending moment can be calculated on the basis of
static structural analysis principles. On the other hand, if the time-varying
load F(t) is applied at the top, the structure is

set to motion or vibration and
experiences accelerations. According to NewtonÕs second law, inertia force is
proportional to acceleration. Inertia forces are proportional to the mass and
they develop in the structure that resists these accelerations. Depending on
the contribution made by inertia force to shear and bending moment will
determine whether dynamic analysis is warranted.
Methodology
A physical problem based on certain assumptions is idealized into a mechanical model by correctly defining in terms of geometry, kinematics and loading and boundary conditions. The governing differential equations are solved to obtain the dynamic response and the results are interpreted in a meaningful manner. For complex structures, it may be necessary to refine the analysis by considering a more detailed mechanical model. In a mechanical model, infinite degrees of freedom are converted to finite degrees of freedom, and for each degree of freedom, exhibiting the structure, there exists a natural frequency at which the structure vibrates in a particular mode of vibration. A mechanical model can also be categorized as either continuous or discrete. Consider a chimney as shown in Fig. 1.3a. In a real structure, the structure manifests distributed mass and stiffness characteristics along the height. The continuous model is shown in Fig. 1.3b. Hence the mathematical continuous model incorporates distributed mass and distributed stiffness to arrive at the response of the system. The displacement v is a function of space and time. On the other hand, we can place the whole mass at the top of the chimney as shown Fig. 1.3c and can consider single-degree-of-freedom (SDOF) in which entire mass m of the structure is localized (lumped) at the top of the structure has constant stiffness k. The independent displacement V(t) is a function of time alone. The lumped mass representation shown in Fig. 1.3d is a three-degrees
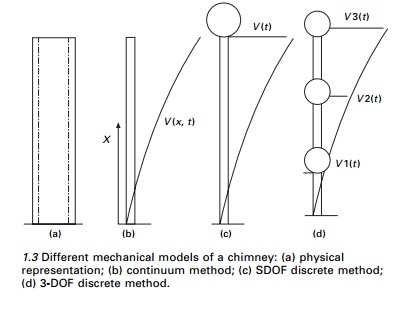
of-freedom system in which each
localized mass m1, m2, m3 has its own displacements V1(t),
V2(t), V3(t) respectively. Practical dynamic
analysis of large complicated multiple-degrees-of-freedom (MDOF) is generally
accomplished by computer-implemented numerical analysis techniques such as the
finite element method.
Types of vibration
Vibration can occur in a structure by imposing
initial conditions, which generally manifest themselves as energy input. If the
initial input is imparting velocity to the system, kinetic energy is produced.
If the displacement is imparted to the system, potential energy is produced. If
the structural vibration occurs in the absence of external loads, it is termed
free vibration. Free vibration usually occurs at the fundamental natural
frequency. Owing to damping present in the system, the free vibration eventually
dampens out. If the vibration takes place under the excitation of external
force, it is called forced vibration. If the source of vibration is periodic,
the resulting vibration may constitute both steady state and transient. Steady
state response transpires at the frequency of excitation. The transient
response is due to the initial energy stored in the structure. A transient
response may also occur if the structure is subjected to blast loads.
Related Topics