Chapter: Civil : Structural dynamics of earthquake engineering
Free and forced vibration of a continuous system
Free and forced vibration of a continuous system in
relation to structural dynamics during earthquakes
Abstract: A
physical system can also be modelled as a continuous system with
distributed mass and stiffness. The governing differential equations of
distributed systems are partial differential equations. In this page,
strings, bars, shafts and beams are modelled as distributed systems and the
dynamic response is studied by solving partial differential equations. Relevant
programs in MATHEMATICA and MATLAB are also given.
Key words: distributed systems, normal
modes, orthogonality, rotary inertia, shear deformation, moving loads.
Introduction
Structures analysed so far have
been treated as discrete systems. In discrete systems stiffness and mass as
well as damping are modelled as discrete properties. Dynamic
analysis of discrete structures will lead to ordinary differential
equations which are amenable to numerical solutions. Another method of
modelling physical systems is based on the distributed mass and stiffness
characteristics. Systems for which stiffness and mass have distributed rather
than discrete properties are referred to as distributed systems or
continuous systems.
If the system is modelled as a distributed system, the
governing differential equations are partial differential equations which are
more difficult to solve. The result obtained from a continuous model is more
accurate than discrete systems. In this chapter, we shall consider the
vibration of simple continuous systems, strings, bars, shafts and beams. It
will readily become apparent, however, that analytical or closed form solutions
can be obtained only for relatively simple continuous systems with well-defined
boundary conditions. In general, the frequency equation of a continuous system
is a transcendental equation that yields an infinite number of natural
frequencies and normal modes. This is in contrast to the behaviour of discrete
systems which yield a finite number of frequencies and mode shapes.
Vibration of a string
Consider a flexible string of
mass Žü/unit length is stretched under
tension T as shown in Fig. 13.1. The dynamic analysis is carried out
based on the following assumptions:
ŌĆó lateral
deflection v is very small;
ŌĆó the
change in tension ŌłåT with
deflection is negligible.
Considering vertical equilibrium of forces we get


A, B, C and D can
be solved depending on initial and boundary conditions. For example if
the string is stretched between two fixed points with distance L, the
boundary conditions are

The mode shape of the string is shown in Fig. 13.2. In the
more general case of free vibration initiated in any manner, the solution will
contain many of the normal modes and the equation for displacement is written
as

Fitting the equation to the
initial conditions v(x, 0), and v˙ ( x, 0)
the values of Cn1, Dn1
can be evaluated.
Longitudinal
vibration of a uniform rod
The rod considered in the section
is thin and uniform along its length. The rod has cross-sectional area A,
modulus of elasticity E and material mass density Žü/unit volume as shown in Fig.
13.3.
The free body diagram of a differential element is shown in Fig.
13.3. In the deformed position the deformed length of dx is dx [1
+ (Ōłéu/Ōłéx) dx].
Summing the horizontal forces the equilibrium equation is written as
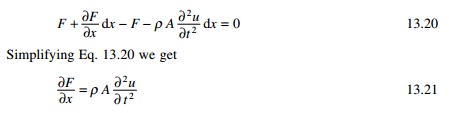
where Ōłé2u/Ōłét2 is the acceleration of
the differential element. Noting that axial force F can be expressed
as

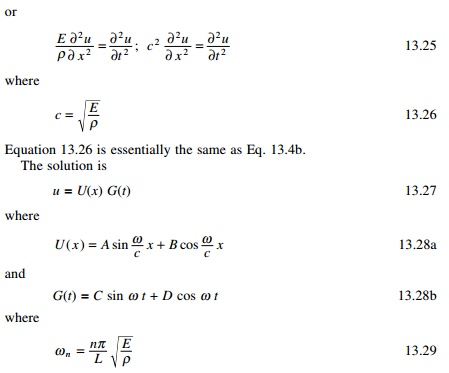
Following the initial conditions
and the boundary conditions the displacement can be obtained at any time t
at any position x.
Example 13.2
Determine expressions for the natural frequencies and
displacement response for longitudinal vibration of a uniform rod with one end
fixed and the other end free as shown in Fig. 13.4.
Example 13.3
Determine the natural frequencies and mode shapes of a
freeŌĆ'free rod (a rod with both ends free).
Example 13.4
Determine the expression for the
natural frequencies and displacement response for longitudinal vibration of a
uniform rod with one end fixed and the other end having a concentrated mass M
as shown in Fig. 13.7. Determine the expression for the frequency equation of
longitudinal vibrations. Length of the rod = L, mass density = Žü, and cross-sectional area = A.
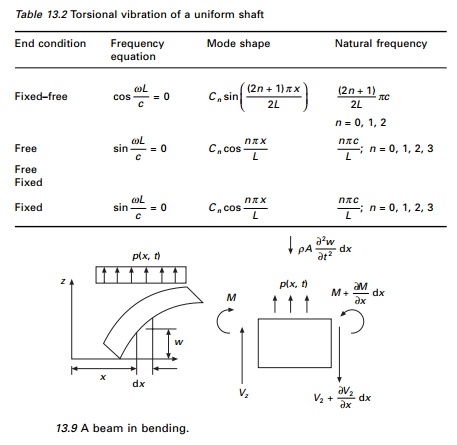
Torsional vibration of shaft
or rod
Figure 13.8 represents a
non-uniform shaft subjected to an external torque m(x, t)/unit
length. If ╬Ė (x,
t) denotes the angle of twist of the cross-section, the relation
between twist and twisting moment Mt (x, t) is
given by
Table 13.1 Values of frequencies
Žē =
╬╗L/c
for various ratios of m/M

where G is the shear
modulus and GJ(x) is the torsional stiffness, with J(x)
denoting polar moment of inertia of the cross-section.
If the mass polar moment of inertia of the
shaft/unit length is I0, the inertia torque acting on an
element of length dx becomes
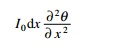
If an external torque mT (x,
t) acts on the shaft/unit length, the application of NewtonŌĆÖs second law
yields

The equation is analogous to the longitudinal vibration of a
rod.
If the shaft is given an initial angular
displacement ╬Ė0(x)
at t = 0, the initial conditions can be stated as

The common boundary conditions
for torsional vibration of uniform shaft are indicated in Table 13.2 along with
corresponding frequency conditions.
Free flexural vibration of
beams
Consider a beam sufficiently long
compared with its cross-section so that shear deformations can be ignored. The
effect of axial load, shear deformation and rotary inertia will be discussed in
the following sections. The free body diagram of a beam segment of element
length dx is shown in Fig. 13.9.
Table 13.2 Torsional vibration
of a uniform shaft
From the elementary theory of bending of beam
(EulerŌĆ'Bernoulli theory)

where E is the YoungŌĆÖs modulus and I
is the moment of inertia of beam cross-section about y-axis. For free
vibration of beams p(x, t) = 0 and hence the equation for
free vibration of non uniform beam is written as
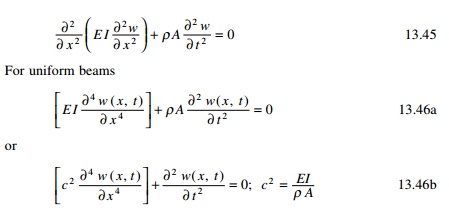
The equation of motion involves a second order
derivative with respect to time and a fourth derivative with respect to x
and hence two initial conditions and four boundary conditions are necessary to
solve the problem. Usually, the values of lateral displacement w0(x)
and w˙ 0 ( x ) at t = 0 so that initial
conditions become


The function W(x) is known as normal
mode or characteristic function of the beam and Žē is the natural frequency of
vibration. For any beam there will be an infinite number of modes with one
natural frequency associated with each normal mode. The unknown values C1,
C2, ŌĆ” C4 and the value of ╬▓ can be determined from the
boundary conditions of the beam as indicated below.

For a beam of length L the deflection,
slope, curvature and d3W/dx3 may be written
at the two ends of the beam (x = 0, x = L) as

The boundary conditions are given in the form of a
matrix as shown below.
Simply supported beam

For a non-trivial solution to exist || BA || = 0 and
the determinant is a function of k and the root of the equation can be
found out. This can very easily be done using the MATHEMATICA package.
Orthogonality of normal
modes
The normal function W(x)
satisfies Eq. 13.51 as

Multiplying Eq. 13.75 by Wj
and Eq. 13.76 by Wi we get

The RHS can be shown to be equal
to zero at x = 0 and x = L. Hence for any combination of
boundary conditions
orthogonality of normal functions
for the transverse vibration of beams.
Effect of axial force
(tension or compression)
The study of vibration of beams
under the action of axial force finds application in the study of vibration of
cables and guy wires. Even though we have treated the cable by an equivalent
string, many cables have failed owing to fatigue caused by alternating flexure,
which is the result of regular shedding of vortices from the cables due to high
wind. Hence it is important to study the vibration of beams due to axial
forces.
Consider the equation of motion
of an element of the beam shown in Fig. 13.12. Writing the equation of
equilibrium for vertical motion we get


For a simply supported beam of
length L the boundary conditions are
W(0) =
W(L) = WŌĆ│(0) =
WŌĆ│(L) = 0 ŌĆ”ŌĆ”ŌĆ”ŌĆ”
13.96
Applying the boundary conditions
C1 = C2
= C4 = 0; and C3 sin
╬▓ L = 0 --- 13.97
╬▓ L = nŽĆ; n = 1, 2, 3ŌĆ” --- 13.97

The natural frequency expressed
in Eq. 13.105 extends the application to single span beams with different
boundary conditions by selecting appropriate value for ╬▓ from Table 13.3. If EI =
0 the problem degenerates to that of a flexible taut cable discussed in Section
13.1. As we see from Eq. 13.105 the tensile load ŌĆśstiffensŌĆÖ the beam,
thereby increasing the natural frequency.
1 Beams subjected
to axial compression
In the above equation substitute
ŌĆ'P for P to get the frequency for a beam subjected to axial
compression:
The following observations can be made:
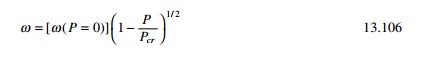
ŌĆó If P
= 0 the natural frequency will be the same as that of a simply supported beam.
ŌĆó If EI
= 0 the frequency reduces to that of a string.
ŌĆó If P
> 0 the natural frequency increases with tensile force as it stiffens the
beams.
ŌĆó If P
< 0 the natural frequency decreases with compressive force and approaches
zero when P = Pcr.
Effect of rotary inertia and shear
deformation
If the cross-sectional dimensions
are not small compared with the length of the beam, we need to consider the
effects of rotary inertia and shear deformation. This was first presented by
Timoshenko and is known as thick beam theory or Timoshenko beam theory.
If the effect of shear
deformation is disregarded (see Fig. 13.13), the tangent to the deflection
centre line OT coincides with the normal to the face BŌĆ▓CŌĆ▓
(since the cross-section normal to the centre line remains normal even after
deformation). Owing to deformation, the tangent to the deformed centre line OŌĆ▓T will not be perpendicular to BŌĆ▓CŌĆ▓.
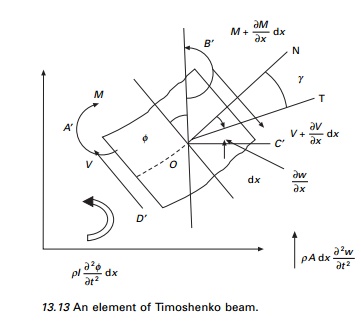
The angle between tangent to the
deformed line OT and normal to the face ON denotes the shear deflection of an
element. Since positive shear on the fight face BŌĆ▓CŌĆ▓ acts downward we have from Fig. 13.13

where Žå denotes the slope of the
deflection curve due to bending deflection alone. Note that because of shear
alone, the element distorts and does not rotate.
The bending moment M and
the shear force V are related to the slope and deflection as
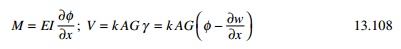
where G denotes the
modulus of rigidity of the material of the beam and ŌĆśkŌĆÖ is a constant
known as TimoshenkoŌĆÖs shear coefficient which depends on the shape of the cross
section. For a rectangular section k = 5/6; circle = 9/10. The equation
of motion can be derived as follows.
1. For translation in the Z
direction

By solving Eq. 13.112a for ŌłéŽå/Ōłéx and substituting the result of Eq. 13.112a in Eq.
112b we obtain (for uniform beams and for free vibration p = 0)

For most practical situations,
the increased accuracy obtained by including shear and rotary effect is much
less than the modelling errors. The contribution for shear stress is generally
less than the contribution for rotation, but both effects can generally be
ignored for shallow beams. The following boundary conditions are to be applied.
Fixed end Žå = w = 0.

Example 13.7
Determine the effects of rotary
inertia and shear deflection on the natural frequency of a simply supported
uniform beam.
Forced axial vibration of bars
Consider a bar as shown in Fig. 13.14 which is
fixed at one end and free at the other end to which an exciting force P(t)
is applied.


A suddenly applied load therefore
produces twice the deflection than that one would obtain if the load is applied
gradually.
Example 13.8
Forced vibration of a flexural member
The simply supported beam shown
in Fig. 13.15a having mass density Žü and cross-sectional area A, moment of inertia I
has a distributed load whose variation with time is shown in Fig. 13.15b.
Determine the expression for dynamic deflection of the beam.
Example 13.9
A simply supported beam carries a
uniformly distributed load of q. Find the resulting vibration of the
beam when the load is suddenly removed.
Beams subjected to moving loads
A particular class of problem
which has long been of interest to engineers involves the determination of the
dynamic response of a beam or girder resulting from the passage of a force or
mass across the span. Examples include the analysis of crane beams and moving
vehicles in highway and railway bridges.
1 Constant force with constant velocity
Let us consider a constant force F moving
across the span of the beam at constant velocity v as indicated in Fig.
13.16. The dynamic deflection may be represented by the summation of modal
components as



where An is the modal amplitude
(which varies with time) and Wn(x) is the
characteristic shape. The velocity is given by
For use in LagrangeŌĆÖs equation, the kinetic energy
T is expressed for the complete system as
The work done by external dynamic force during an
arbitrary distortion is
where CF is the distance from the end of
the span to the force.
Using Lagrange equation of equilibrium as
CF is a function of time. Assume the
beam to be prismatic and simply supported
Example 13.10
Derive the mid-span deflection of a simple beam
traversed by a constant force, ignoring damping and including only a
fundamental mode (higher modes are of negligible importance). The parameters of
the system are given as M = 2 kg; EI = 78 700 N m2, L
= 10 m, v = 12.5 m/s. Calculate the critical speed to cause resonance.
The first term of the above
expression is forced and the second one is free vibration. The deflection is
plotted in Fig. 13.17 as a fraction of mid-span deflection. The abscissa may be
considered to be either time or the position of load on the span. Plotted
separately is the forced part of the solution which is very nearly equal to the
static deflection ordinates of Fig. 13.17 may also be regarded as the ratio of
dynamic to static moments.
Summary
The dynamic analysis of string, bar and beam with
distributed properties (mass and elasticity) and subjected to various types of
loading were presented in this chapter. The extension of the analysis to
multi-span continuous beams, though possible, is complex and impractical. The
results obtained from these single span beams are particularly important in
evaluating an approximate method based on discrete models.
Related Topics