Response spectra

Distinction between design and response spectra

A design spectrum conceptually differs from a response spectrum in two ways. A response spectrum is a jagged plot of peak response of all possible

SDOF systems, and hence is a description of a particular ground motion. A design spectrum is smooth and is the envelope of the different elastic design spectra. Figure 17.27 shows a design spectrum as the envelope of design spectra for earthquakes originating on the different faults. The conceptual differences between the response obtained from the response spectrum and design spectrum are demonstrated in Fig. 17.27. In this figure, notice that for some periods these values obtained for response and design spectra are the same, and for some other periods there is a considerable discrepancy. In general, the response spectrum and the design spectrum do not yield the same result since the former represents the response to a specific earthquake, while the latter represents only the predicted response to an earthquake having the same PGA (peak ground acceleration).

Response spectrum

1Acceleration, velocity and displacement spectrum

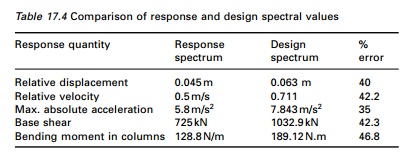
With the pseudo-velocity design spectrum (see Fig. 17.28), the pseudo-acceleration design spectrum and deformation design spectrum are determined from the equation

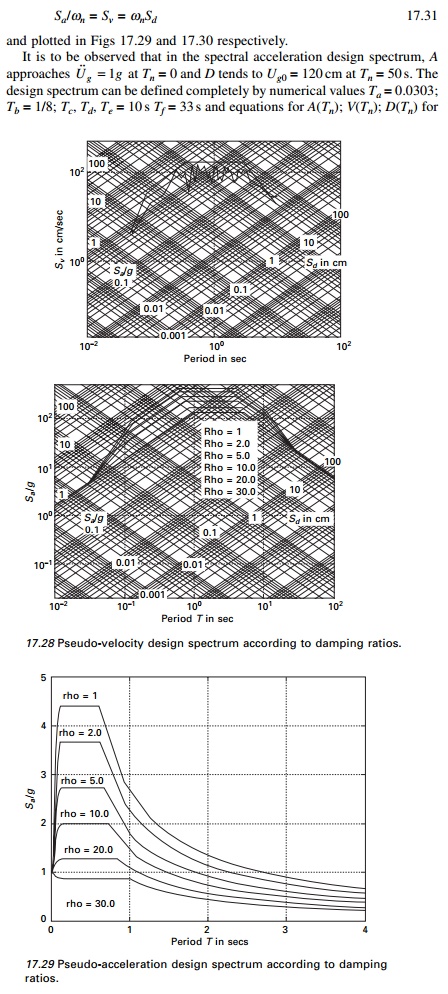
each branch of the spectra. Out of six periods, four of them in T_a; T_b; T_e; T_f are fixed but the others T_c; T_d depend on damping. Equations describing various branches of the pseudo-acceleration design spectrum are given in Fig. 17.23. Observe that the pseudo-acceleration design spectrum for 84.1%

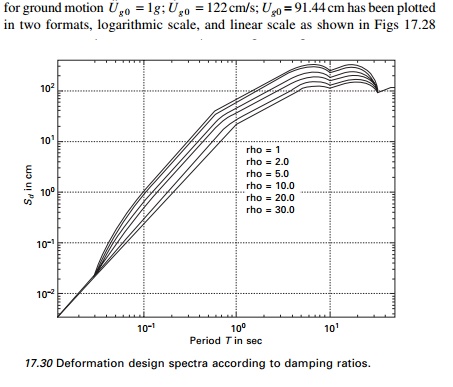
and 17.29. The two plots include spectrum values for six different damping values 1%, 2% , 5%, 10%, 20% and 30% respectively. Scaling the spectrum by η is the simplest way to obtain design spectra for ground motion of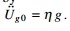 

2Peak structural response from spectrum

It is possible to get a peak response of SDOF from the response spectrum without computing the response history. Corresponding to the natural vibration period T_n and damping ratio ρ, the values of D, V and A are read from the spectrum of Fig. 17.23.

Peak values of elastic static force f_s0

f_s0 = mA = kD = mg(a/g) = WA/g    --- ---- 17.32

For a one storey structure shown in Fig. 17.31 the base shear is calculated as

Base shear can be obtained out of the D, V, A spectrum. One of D, V, A needs to be obtained in structural design.

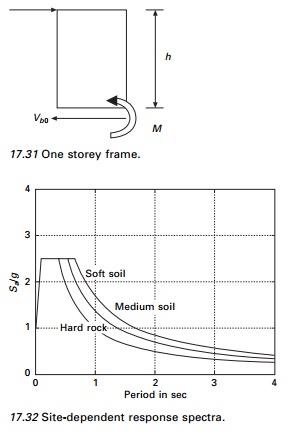
Site-specific response spectra

The design spectra such as those presented above were based on earthquake records on alluvium and did not consider soil condition as a parameter. It is concluded from various studies that soil condition at a site significantly affects the amplifications and shapes as illustrated in Fig. 17.32. Thus the ground motions near the surface where a structure may be located are affected by the properties of the soil (e.g., stiffness, strength and layering) and the rock strata between the site and the source. The available data suggest that there is a major difference between spectral amplification factors calculated on soft soils and those calculated in competent rock. In relatively soft soils, spectral specifications vary with the frequency and intensity of ground motion, and spectral velocities and accelerations may be twice those of competent rock. In extremely soft soil the accelerations may decrease slightly but spectral displacements and velocities may increase by a factor of 2 compared with the rock.

To account for variability in the soil condition at the site in an approximate  manner, modification factors for the spectral amplification factors are presented in Table 17.5. For especially important structures or where local conditions are not amenable to simple classification, the use of smooth spectra curves is inadequate. In such cases, site-specific studies are performed to determine more precisely the expected intensity and character of seismic motion. It is necessary to be aware of the procedure used in the generation of site-specific response spectra. At a site, the maximum capable earthquake (MCE) is selected as the largest earthquake reasonably likely to occur. The slip rates of the faults are eliminated with some probability. Using a statistical approach the peak ground acceleration, velocity and displacement values are estimated at a site. By applying structure amplification factors to these values the spectral bounds are obtained for each desired value of spectral damping. The ground motion values for a given site thus vary with the magnitude of the earthquake and the distance of the site from the point of energy release. These values provide the basis for developing site-dependent response spectrum curves as shown in Fig. 17.32.