Chapter: 11th 12th std standard Class Physics sciense Higher secondary school College Notes
Radioactive displacement law
Radioactive displacement law
During a radioactive disintegration, the
nucleus which undergoes disintegration is called a parent nucleus and that
which remains after the disintegration is called a daughter nucleus. In 1913,
Soddy and Fajan framed the displacement laws governing radioactivity.
α-decay
When a radioactive nucleus disintegrates by
emitting an α-particle,
the atomic number decreases by two and mass number decreases by four. The α-decay can be expressed as
zXA → z−2YA−4 + 2He4
Example : Radium (88Ra226)
is converted to radon (86Rn222) due to α−decay
88Ra226
→ 86Rn222
+ 2He4
β−decay
When a radioactive nucleus disintegrates by
emitting a β−
particle, the atomic number increases by one and the mass number remains the
same. β−decay
can be expressed as
zXA
→ Z+1YA
+ −1e0
Example : Thorium (90Th234)
is converted to protoactinium (91Pa234) due to β−decay
90Th234 → 91Pa234
+ −1e0
At a time, either α or β−particle
is emitted. Both α and β particles are not emitted during a single decay.
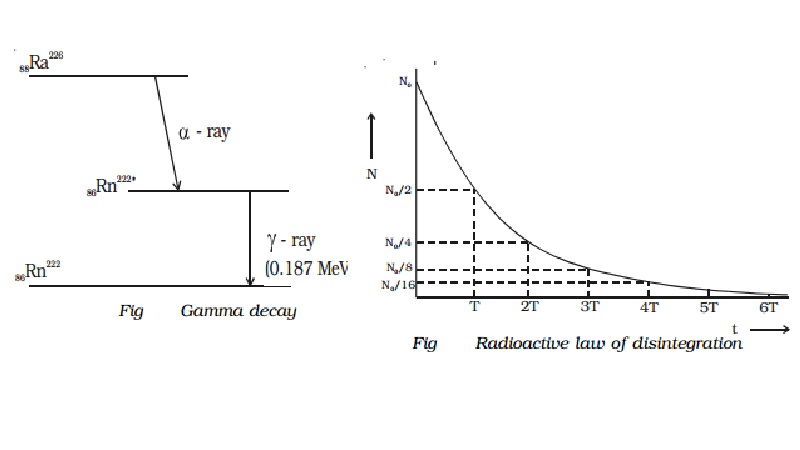
γ−decay
When a radioactive nucleus emits γ−rays, only the energy level of the nucleus changes and the 88 atomic number and mass number remain the
same.
During α or β−decay, the daughter nucleus is mostly in the excited state.
It comes to ground state with the
emission of γ−rays.
Example : During the radioactive disintegration of radium (88Ra226) into radon (86Rn222), gamma ray of energy 0.187 MeV is emitted, when radon returns from the excited state to the ground state (Fig.)
Radioactive law of disintegration
Rutherford and Soddy found that the rate of disintegration is
independent of physical and chemical conditions. The rate of disintegration at
any instant is directly proportional to the number of atoms of the element present at that instant.
This is known as radioactive law of disintegration.
Let N0 be the number of radioactive atoms present
initially and N, the number of atoms at a given instant t. Let dN be the number
of atoms undergoing disintegration in a small interval of time dt. Then the
rate of disintegration is
-dN/dt ∝ N
dN/dt = -
λN …………….(1)
where λ is a constant known as decay constant or disintegration constant.
The negative sign indicates that N decreases with increase in time.
Equation
(1) can be written as
dN/N = -
λ dt
Integrating,
loge N = - λt + C …… (2)
where C
is a constant of integration.
At t =
0, N = N0
loge
No = C
Substituting for C, equation (2) becomes
loge N = −λt + loge N0
loge(N/N0)
= −λt
N/N0=
e−λt
N= N0 e−λt
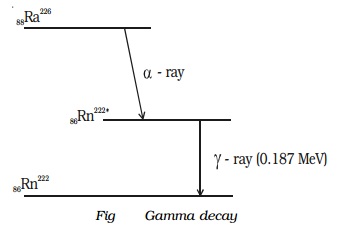
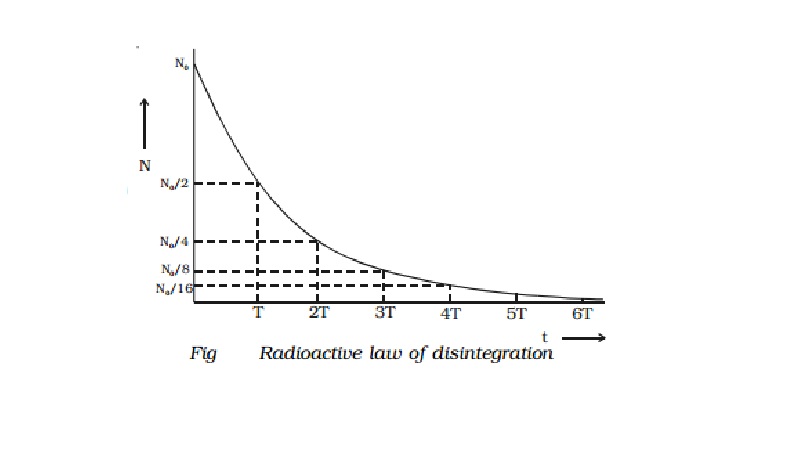
Equation
(3) shows that the number of atoms of a radioactive subs tance decreases expo
nentially with increa se in time (Fig)
Initially the disintegration takes place at a faster
rate. As time increases, N gradually decreases exponentially. Theoretically, an
infinite time is required for the complete disintegration of all the atoms.
Half life period
Since all the radioactive elements have
infinite life period, in order to distinguish the activity of one element with
another, half life period and mean life period are introduced.
The half life period of a radioactive element
is defined as the time taken for one half of the radioactive element to undergo
disintegration.
From the
law of disintegration
N = N0e−λt
T½
= loge2 / λ = 0.6931/ λ
The half life period is inversely proportional
to its decay constant. The concept of half time period can be understood from
Fig..
For a radioactive substance, at the end of T½,
50% of the material remain unchanged. After another T½ i.e., at the
end of 2 T½, 25% remain unchanged. At the end of 3 T½,
12.5% remain unchanged and so on.
Mean life
When the radioactive substance is undergoing
disintegration, the atom which disintegrates at first has zero life and that
disintegrates at last has infinite life. The actual life of each atom ranges
from zero to infinity.
The mean life of a radioactive substance is defined as the ratio of
total life time of all the radioactive atoms to the total number of atoms in
it.
Mean life = Sum of life time of all the atoms / Total
number of atoms
The mean life is calculated from the law of disintegration and it
can be shown that the mean life is the reciprocal of the decay constant.
τ = 1/λ
The half life and mean life
are related as
T½ = 0.6931 / λ = 0.6931 τ
Activity
The activity of a radioactive substance is
defined as the rate at which the atoms decay. If N is the number of atoms present at a certain time t, the activity R is given by
R = dN
/dt
The unit of activity is becquerel named after
the scientist Henri Becquerel
1 becquerel = 1 disintegration per second
The activity of a radioactive substance is
generally expressed in curie. Curie is defined as the quantity of a radioactive
substance which gives 3.7 × 1010 disintegrations per second or 3.7 ×
1010 becquerel. This is equal to the activity of one gram of radium.
Related Topics