Chapter: 11th 12th std standard Class Physics sciense Higher secondary school College Notes
Proof and Applications of Law of conservation of momentum
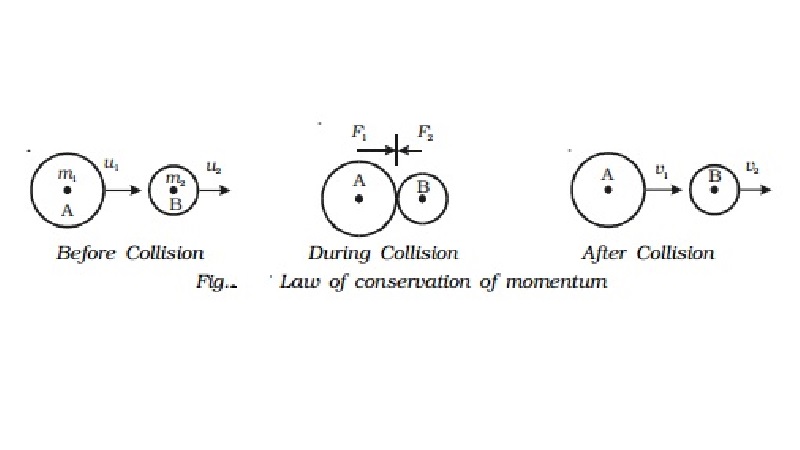
Law of conservation of momentum
From the principle of impulse and momentum, impulse of a force, J = mv - mu
If J = 0 then mv - mu = 0 (or) mv = mu
(i.e) final momentum = initial momentum
In general, the total momentum of the system is always a constant (i.e) when the impulse due to external forces is zero, the momentum of the system remains constant. This is known as law of conservation of momentum.
We can prove this law, in the case of a head on collision between two bodies.
Proof
Consider a body A of mass m1 moving with a velocity u 1 collides head on with another body B of mass m2 moving in the same direction as A with velocity u2 as shown in Fig.
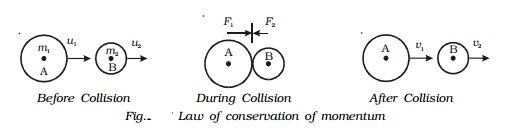
After collision, let the velocities of the bodies be changed to v1 and v2 respectively, and both moves in the same direction. During collision, each body experiences a force.
The force acting on one body is equal in magnitude and opposite in direction to the force acting on the other body. Both forces act for the same interval of time.
Let F1 be force exerted by A on B (action), F2 be force exerted by B on A (reaction) and t be the time of contact of the two bodies during collision.
Now, F1 acting on the body B for a time t, changes its velocity from u2 to v2.
∴ F1 = mass of the body B x acceleration of the body B
= m2 x(v2-u2)/t ............(1)
Similarly, F2 acting on the body A for the same time t changes its velocity from u1 to v1
∴ F2 = mass of the body A x acceleration of the body A
= m1 x (v1-u1)/t ...........(2)
Then by Newton's third law of motion F1 = �'F2
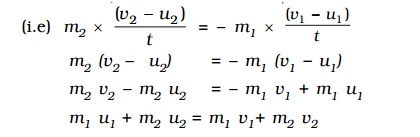
m1 u1 + m2 u2 = m1 v1+ m2 v2 ...........(3)
(i.e) total momentum before impact = total momentum after impact.
(i.e) total momentum of the system is a constant.
This proves the law of conservation of linear momentum.
Applications of law of conservation of momentum
The following examples illustrate the law of conservation of momentum.
(i) Recoil of a gun
Consider a gun and bullet of mass mg and mb respectively. The gun and the bullet form a single system. Before the gun is fired, both the gun and the bullet are at rest. Therefore the velocities of the gun and bullet are zero. Hence total momentum of the system before firing is mg(0) + mb(0) = 0
When the gun is fired, the bullet moves forward and the gun recoils backward. Let vb and vg are their respective velocities, the total momentum of the bullet - gun system, after firing is mbvb + mgvg
According to the law of conservation of momentum, total momentum before firing is equal to total momentum after firing.
(i.e) 0 = mb vb + mgvg
(Or)
vg =( mb/mg ). vb
It is clear from this equation, that vg is directed opposite to vb. Knowing the values of mb, mg and vb, the recoil velocity of the gunvg can be calculated.
(ii) Explosion of a bomb
Suppose a bomb is at rest before it explodes. Its momentum is zero. When it explodes, it breaks up into many parts, each part having a particular momentum. A part flying in one direction with a certain momentum, there is another part moving in the opposite direction with the same momentum. If the bomb explodes into two equal parts, they will fly off in exactly opposite directions with the same speed, since each part has the same mass.
Related Topics