Chapter: 11th 12th std standard Class Physics sciense Higher secondary school College Notes
Newton's third Law of motion
Newton's third Law of motion
It is a common observation that when we sit on a chair, our body exerts a downward force on the chair and the chair exerts an upward force on our body. There are two forces resulting from this interaction: a force on the chair and a force on our body. These two forces are called action and reaction forces. Newton's third law explains the relation between these action forces. It states that for every action, there is an equal and opposite reaction.
(i.e.) whenever one body exerts a certain force on a second body, the second body exerts an equal and opposite force on the first. Newton's third law is sometimes called as the law of action and reaction.
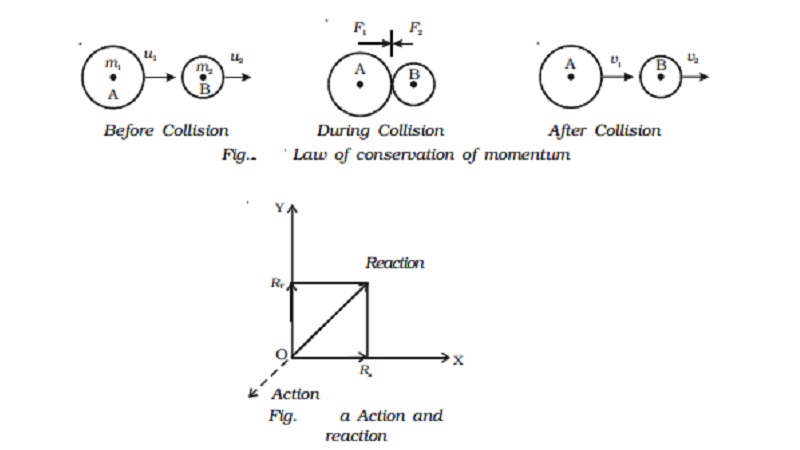
Let there be two bodies 1 and 2 exerting forces on each other. Let the force exerted on the body 1 by the body 2 be Vector F21 and the force exerted on the body 2 by the body 1 be Vector F21. Then according to third law, Vector F21 = - Vector F21.
One of these forces, say Vector F21 may be called as the action whereas the other force Vector F21 may be called as the reaction or vice versa. This implies that we cannot say which is the cause (action) or which is the effect (reaction). It is to be noted that always the action and reaction do not act on the same body; they always act on different bodies. The action and reaction never cancel each other and the forces always exist in pair.
The effect of third law of motion can be observed in many activities in our everyday life. The examples are
i. When a bullet is fired from a gun with a certain force (action), there is an equal and opposite force exerted on the gun in the backward direction (reaction).
ii. When a man jumps from a boat to the shore, the boat moves away from him. The force he exerts on the boat (action) is responsible for its motion and his motion to the shore is due to the force of reaction exerted by the boat on him.
iii. The swimmer pushes the water in the backward direction with a certain force (action) and the water pushes the swimmer in the forward direction with an equal and opposite force (reaction).
iv. We will not be able to walk if there were no reaction force. In order to walk, we push our foot against the ground. The Earth in turn exerts an equal and opposite force. This force is inclined to the surface of the Earth. The vertical component of this force balances our weight and the horizontal component enables us to walk forward.
v. A bird flies by with the help of its wings. The wings of a bird push air downwards (action). In turn, the air reacts by pushing the bird upwards (reaction).
vi. When a force exerted directly on the wall by pushing the palm of our hand against it (action), the palm is distorted a little because, the wall exerts an equal force on the hand (reaction).
Law of conservation of momentum
From the principle of impulse and momentum, impulse of a force, J = mv - mu
If J = 0 then mv - mu = 0 (or) mv = mu
(i.e) final momentum = initial momentum
In general, the total momentum of the system is always a constant (i.e) when the impulse due to external forces is zero, the momentum of the system remains constant. This is known as law of conservation of momentum.
We can prove this law, in the case of a head on collision between two bodies.
Proof
Consider a body A of mass m1 moving with a velocity u 1 collides head on with another body B of mass m2 moving in the same direction as A with velocity u2 as shown in Fig.
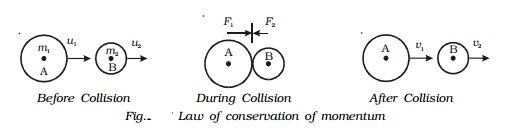
After collision, let the velocities of the bodies be changed to v1 and v2 respectively, and both moves in the same direction. During collision, each body experiences a force.
The force acting on one body is equal in magnitude and opposite in direction to the force acting on the other body. Both forces act for the same interval of time.
Let F1 be force exerted by A on B (action), F2 be force exerted by B on A (reaction) and t be the time of contact of the two bodies during collision.
Now, F1 acting on the body B for a time t, changes its velocity from u2 to v2.
∴ F1 = mass of the body B x acceleration of the body B
= m2 x(v2-u2)/t ............(1)
Similarly, F2 acting on the body A for the same time t changes its velocity from u1 to v1
∴ F2 = mass of the body A x acceleration of the body A
= m1 x (v1-u1)/t ...........(2)
Then by Newton's third law of motion F1 = �'F2
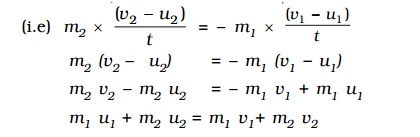
m1 u1 + m2 u2 = m1 v1+ m2 v2 ...........(3)
(i.e) total momentum before impact = total momentum after impact.
(i.e) total momentum of the system is a constant.
This proves the law of conservation of linear momentum.
Applications of law of conservation of momentum
The following examples illustrate the law of conservation of momentum.
(i) Recoil of a gun
Consider a gun and bullet of mass mg and mb respectively. The gun and the bullet form a single system. Before the gun is fired, both the gun and the bullet are at rest. Therefore the velocities of the gun and bullet are zero. Hence total momentum of the system before firing is mg(0) + mb(0) = 0
When the gun is fired, the bullet moves forward and the gun recoils backward. Let vb and vg are their respective velocities, the total momentum of the bullet - gun system, after firing is mbvb + mgvg
According to the law of conservation of momentum, total momentum before firing is equal to total momentum after firing.
(i.e) 0 = mb vb + mgvg
(Or)
vg =( mb/mg ). vb
It is clear from this equation, that vg is directed opposite to vb. Knowing the values of mb, mg and vb, the recoil velocity of the gunvg can be calculated.
(ii) Explosion of a bomb
Suppose a bomb is at rest before it explodes. Its momentum is zero. When it explodes, it breaks up into many parts, each part having a particular momentum. A part flying in one direction with a certain momentum, there is another part moving in the opposite direction with the same momentum. If the bomb explodes into two equal parts, they will fly off in exactly opposite directions with the same speed, since each part has the same mass.
Applications of Newton's third law of motion
(i) Apparent loss of weight in a lift
Let us consider a man of mass M standing on a weighing machine placed inside a lift. The actual weight of the man = Mg. This weight (action) is measured by the weighing machine and in turn, the machine offers a reaction R. This reaction offered by the surface of contact on the man is the apparent weight of the man.
Case (i)
When the lift is at rest:
The acceleration of the man = 0
Therefore, net force acting on the man = 0
From Fig. (i), R - Mg = 0 (or) R = Mg

That is, the apparent weight of the man is equal to the actual weight.
Case (ii)
When the lift is moving uniformly in the upward or downward direction:
For uniform motion, the acceleration of the man is zero. Hence, in this case also the apparent weight of the man is equal to the actual weight.
Case (iii)
When the lift is accelerating upwards:
If a be the upward acceleration of the man in the lift, then the net upward force on the man is F = Ma
From Fig (ii), the net force
F = R - Mg = Ma (or) R = M ( g + a )
Therefore, apparent weight of the man is greater than actual weight.
Case (iv)
When the lift is accelerating downwards:
Let a be the downward acceleration of the man in the lift, then the net downward force on the man is F = Ma
From Fig. (iii), the net force
F = Mg - R = Ma (or) R = M (g + a)
Therefore, apparent weight of the man is less than the actual weight.
When the downward acceleration of the man is equal to the acceleration due to the gravity of earth, (i.e) a = g
∴ R = M (g - g) = 0
Hence, the apparent weight of the man becomes zero. This is known as the weightlessness of the body.
(ii) Working of a rocket and jet plane
The propulsion of a rocket is one of the most interesting examples of Newton's third law of motion and the law of conservation of momentum.
The rocket is a system whose mass varies with time. In a rocket, the gases at high temperature and pressure, produced by the combustion of the fuel, are ejected from a nozzle. The reaction of the escaping gases provides the necessary thrust for the launching and flight of the rocket.
From the law of conservation of linear momentum, the momentum of the escaping gases must be equal to the momentum gained by the rocket. Consequently, the rocket is propelled in the forward direction opposite to the direction of the jet of escaping gases. Due to the thrust imparted to the rocket, its velocity and acceleration will keep on increasing. The mass of the rocket and the fuel system keeps on decreasing due to the escaping mass of gases.
Related Topics