Motion in one dimension (rectilinear motion)

Motion in one dimension (rectilinear motion)

The motion along a straight line is known as rectilinear motion. The important parameters required to study the motion along a straight line are position, displacement, velocity, and acceleration.

1.Position, displacement and distance travelled by the particle

The motion of a particle can be described if its position is known continuously with respect to time.

The total length of the path is the distance travelled by the particle and the shortest distance between the initial and final position of the particle is the displacement.

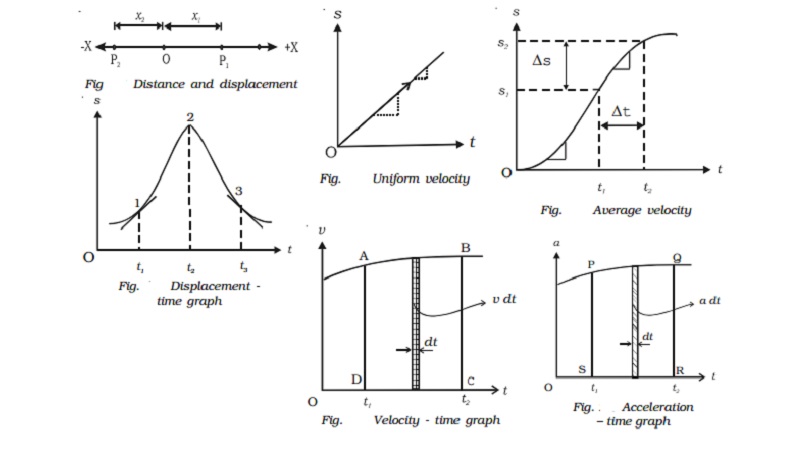
The distance travelled by a particle, however, is different from its displacement from the origin. For example, if the particle moves from a Fig 2.1 Distance and displacement point O to position P1 and then to position P₂, its displacement at the position P₂ is ? x₂ from the origin but, the distance travelled by the particle is x₁+x₁+x₂ = (2x₁+x₂) (Fig ).

The distance travelled is a scalar quantity and the displacement is a vector quantity.

2 Speed and velocity

Speed

It is the distance travelled in unit time. It is a scalar quantity.

Velocity

The velocity of a particle is defined as the rate of change of displacement of the particle. It is also defined as the speed of the particle in a given direction. The velocity is a vector quantity. It has both magnitude and direction.

Velocity = displacement / time taken

Its unit is m s-¹  and its dimensional formula is   LT^-1

A particle is said to move with uniform velocity if it moves along a fixed direction and covers equal displacements in equal intervals of time, however small these intervals of time may be.

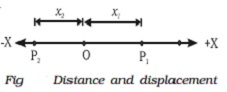
In  a  displacement  -  time  graph, _t (Fig. ) the slope is constant at all the points, when the particle moves with uniform velocity.

Non uniform or variable velocity

The velocity is variable (non-uniform), if it covers unequal displacements in equal intervals of time or if the direction of motion changes or if both the rate of motion and the direction change.

Average velocity

Let s1 be the displacement of a body in time t ₁ and s₂ be itsdisplacement in time t ₂ (Fig.).

The average velocity during the timeinterval (t₂ ? t₁) is defined as

v_average = change in displacement / change in time

= s₂-s₁ / t₂-t₁  = ∆s / ∆t

From the graph, it is found that the slope of the curve varies.

Instantaneous velocity

It is the velocity at any given instant of time or at any given point of its path. The instantaneous velocity v is given by

v= Lim  ∆s / ∆t =  ds / dt

3. Acceleration

If the magnitude or the direction or both of the velocity changes with respect to time, the particle is said to be under acceleration.

Acceleration of a particle is defined as the rate of change of velocity. Acceleration is a vector quantity.

Acceleration = change in velocity / time taken

If u is the initial velocity and v, the final velocity of the particle after a time t, then the acceleration,

A = ( v-u )/ t

Its unit is m s⁻² and its dimensional formula is LT⁻².

The instantaneous acceleration is , a= dv/dt = d/dt(ds/dt) = d²s/dt²

Uniform acceleration

If the velocity changes by an equal amount in equal intervals of time, however small these intervals of time may be, the acceleration is said to be uniform.

Retardation or deceleration

If the velocity decreases with time, the acceleration is negative. The negative acceleration is called retardation or deceleration.

Uniform motion

A particle is in uniform motion when it moves with constant velocity (i.e) zero acceleration.

4 Graphical representations

The graphs provide a convenient method to present pictorially, the basic informations about a variety of events. Line graphs are used to show the relation of one quantity say displacement or velocity with another quantity such as time.

If the displacement, velocity and acceleration of a particle are plotted with respect to time, they are known as,

1.  displacement ? time graph (s - t graph)

2.    velocity ? time graph (v - t graph)

3.      acceleration ? time graph (a - t graph)

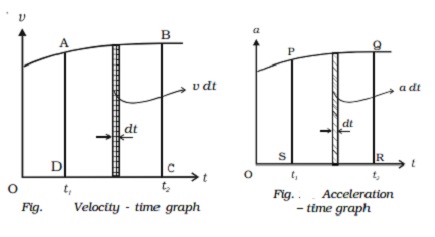
Displacement ? time graph When the displacement of the particle is plotted as a function of time, it is  displacement - time graph.

As v = ds/dt , the slope of the s - t graph at any instant gives the velocity of the particle at that instant. In Fig.  the particle at time t1, has a positive velocity, at time t2, has zero velocity and at time t3, has negative velocity.

Velocity ? time graph

When the velocity of the particle is plotted as a function of time, it is velocity-time graph.

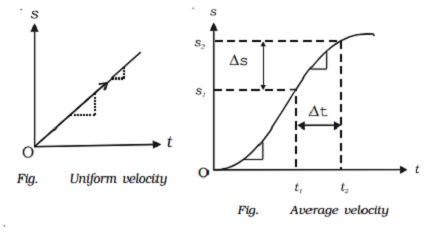
As a = dv/dt , the slope of the v ? t curve at any instant gives the acceleration of the particle (Fig. ).

But v=ds/dt or

Ds = v dt

If the displacements are s₁ and s₂ in times t₁ and t₂ then

∫₁²ds = ∫ _t1^t2 vdt

S₂-s₁ = ∫_t1^t2vdt = area ABCD

The area under the v ? t curve, between the given intervals of time, gives the change in displacement or the distance travelled by the particle during the same interval.

Acceleration ? time graph

When the acceleration is plotted as a function of time, it is acceleration ? time graph (Fig. ).

A=dv/dt 

Or dv = adt

If the velocities are v₁ and v₂ at times t₁ and t₂ respectively, then

∫_v1^v2 dv = ∫_t1^t2 a dt

V₂-v₁ = ∫_t1^t2adt =  area PQRS

The area under the a ? t curve, between the given intervals of time, gives the change in velocity of the particle during the same interval. If the graph is parallel to the time axis, the body moves with constant

acceleration.

5 Equations of motion

For uniformly accelerated motion, some simple equations that relate displacement s, time t, initial velocity u, final velocity v and acceleration a are obtained.

(i) As acceleration of the body at any instant is given by the first derivative of the velocity with respect to time,

A=dv/dt  or dv=adt

If the velocity of the body changes from u to v in time t then from the above equation.

∫_u^vdv = ∫₀^t adt = a∫₀^tdt =

[v]_u^v = a[t]₀^t

v-u =at

v=u+at

(ii) The velocity of the body is given by the first derivative of the displacement with respect to time.

v=ds/dt

ds=vdt

Since v = u + at, ds = (u + at) dt

The distance s covered in time t is,

∫₀^sds = ∫₀^tudt+∫₀^tatdt

S=ut+1/2at²

(iii) The acceleration is given by the first derivative of velocity with respect to time. (i.e)

A=dv/dt=dv/ds.ds/dt = dv/ds.v

Ds=1/a.vdv

Therefore,

∫₀^sds =∫_u^v(vdv)/a

S=1/2a(v²-u²)

Or

2as=v²-u²

v²=u²+2as

The equations (1), (2) and (3) are called equations of motion.

Expression for the distance travelled in n^th second

Let a body move with an initial velocity u and travel along a straight line with uniform acceleration a.

Distance travelled in the nth second of motion is,

S_n = distance travelled during first n seconds ? distance

travelled during (n ?1) seconds

Distance travelled during n seconds

D_n=un+1/2an²

Distance travelled during (n -1) seconds

D_(n-1) = u(n+1) + 1/2a(n-1)²

the distance travelled in the nth second = D_n− D_{(n ?1)}

S_n = (un+1/2an²).[u(n-1)+1/2a(n-1)²]

S_n=u+1/2a(2n-1)

Special Cases

Case (i) : For downward motion

For a particle moving downwards, a = g, since the particle moves in the direction of gravity.

Case (ii) : For a freely falling body

For a freely falling body,    a = g and u =   0, since it starts from rest.

Case (iii) : For upward motion

For a particle moving upwards, a = - g, since the particle moves against the gravity.