Chapter: Civil : Structural dynamics of earthquake engineering
Modal response contribution using ChopraŌĆÖs method
Modal response contribution
using ChopraŌĆÖs method (Chopra, 2002)
The forced vibration of undamped
system and the dynamic equation of motion may be written as
mu˙˙ + ku =
F (t ) --- ---
18.22
We now consider the common
loading case in which the force Fj(t) have the same
time variation f (t) and their spatial distribution is defined, independent
of time. Thus
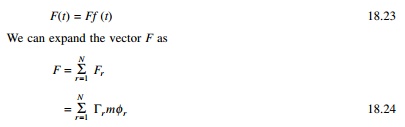
where Žår is the
normalized eigenvector for the rth mode.
Pre-multiplying both sides with ŽånT and
utilizing the orthogonalization property of the modes we get

which is independent of how the modes are normalized.
Equation 18.26 may be viewed as
an expression of the distribution F of applied force in terms of force
distribution Fn associated with natural period. This
interpretation becomes apparently clear by considering the structure vibration
in the n th mode with acceleration u╦Ö╦Ön = Žån ╦Ö╦Öyn
( t ) . The associated inertia force = ŌłÆ
mu╦Ö╦Ön (t ) = ŌłÆ mŽån ╦Ö╦Öyn
and their spatial distribution given by vector mŽån which is
same as Fn.
Two
useful properties are to be noted:
1. The force
vector Fn f (t) produces response only in the nth
mode, there is no response in another mode.
2. This
dynamic response in the nth mode is entirely due to the partial force
vector Fnp(t).
Example 18.4
Consider a five storey building
(rigid floor beams and slabs) with lumped mass m at each floor, and same
storeyed stiffness k. <F>= <0 0 ŌĆō1 1 2). See Fig. 18.8.
Solution
Use the MATHEMATICA or MATLAB
package. Assume k = 1 m = 1.
Using the MATLAB program we get
five natural frequencies and five normalized mode shapes.
Žē1 = 0.2439; Žē2 =
0.6689; Žē3 = 1.0; Žē4 = 1.286;
Žē5 = 1.6850
rad/s
Modal analysis for ╬ō f (t)

The factor ╬ōn which
multiplies the force f (t) is sometimes known as the modal
participation factor, implying that it is a measure of the degree to which the nth
mode participates in the response. This is not a useful definition because ╬ōn is not
independent of how the mode is normalized or a measure of the contribution of
the mode to a response quantity. Both these drawbacks are overcome by the modal
contribution factor.
Let us consider the uncoupled
equation of motion
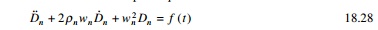
Hence yn is
readily available once equation 18.30 has been solved for Dn
(t) utilizing the available result of single-degree-of-freedom (SDOF)
systems say, for example, subjected to harmonic step impulsive forces, etc.

which is the contribution of the nth
mode of modal displacement u(t). Substituting Eq. 18.30 to get
the equivalent static force as

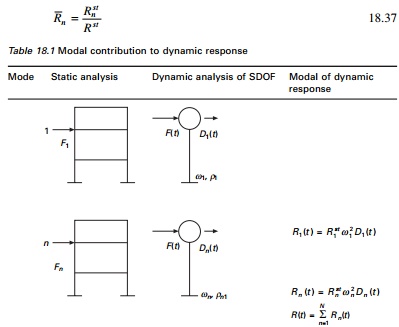
The nth mode contribution
to any response quantity R(t) is determined by static analysis of
structures subjected to forces fn(t). If Rnst
denotes the modal static response, the static value indicating ŌĆśstŌĆÖ of R
due to external force Fn then
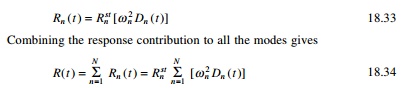
The model analysis procedure just
presented is a special case of the one presented earlier. It has the advantage
of providing a basis for identifying and understanding the factors that
influence the relative modal contributions to the response. The above procedure
can be applied only if the f (t) for all the forces are the same.
Interpretation of modal
analysis
1. Determine
natural frequencies and modes.
2. Force
distribution is expanded into modal components {F}.
The rest of the procedure is explained in Table 18.1.
Modal contribution factor
The contribution Rn
of the nth mode to response quantity R can be expressed
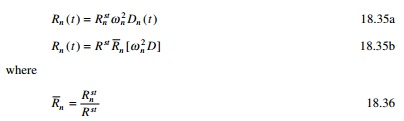
where Rst is
the static value of R due to external force F and the nth
modal contribution factor is defined as
These modal contribution factors have three important
properties:
1. They are
dimensionless.
2. They are
independent of how modes are normalized.
3. The sum
of modal contribution factors over all modes is unity.

Modal response and required number of modes
Consider the displacement Dn(t)
of the nth mode SDOF system. The peak value is defined as
Dn0 = Max t| Dn(t) | --- ---18.39a
The corresponding value Rn(t)
is

The algebraic system of Rno
is same as the modal static response Rnst = R st Rn . The
modal contribution factor dynamic response factor R(t) influences
the relative response contribution of vibration mode, and hence the minimum
number of modes that should be included in dynamic analysis. If only J
modes are included in the static response

For a fixed J, ej
depends on spatial distribution of F of the applied force. When all
modes are included ej = 0. Hence modal analysis can truncate
modes when | ej | < ╬Ą. Hence
most important factors are modal contribution factor and dynamic response
factors.
Modal contributions

For the five storey situation
three modes are required for base shear and two modes are required for roof
displacement.
Example 18.5
For the five storey building example
F(t)
= Ff (t); < F >=< 0 0 ŌĆō 1 1 2>
The system is undamped. Compute only the steady state
response.
Example 18.6
Figure 18.11 shows a shear frame
(i.e. rigid beams) and its floor masses and storey stiffness. This structure is
subjected to horizontal harmonic force at the top floor. p0 =
500 kN.
(a) Determine
the equation for steady state displacement of the structure.
(b) Determine
the direct solution of coupled equations.
(c) Determine
the modal analysis (neglect damping).
(d) If k
= 63 600 kN/m, m = 45 413 kg and Žē = 0.75 Žē1 split
the load into modal components and obtain the solution using ChopraŌĆÖs method.
Solution
Example 18.7
Figure 18.13 shows a mass-less
simply suported beam with three lumped masses and the following properties: L
= 3.81 m, m = 33 665 kg, E = 207.15 GPa.
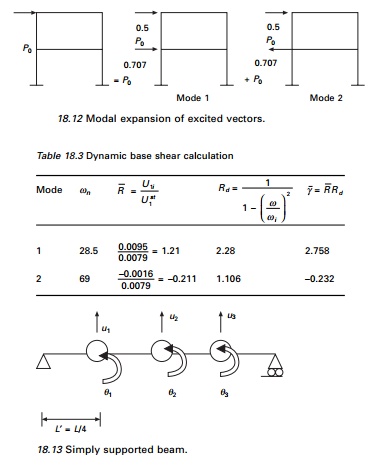
We are interested in studying the
dynamic response of the beam to F(t) = Ff(t) where
< F >=<1 0 0>.
(a) Determine
the modal expansion of vector {F} that defines the spatial distribution
of force.
(b)For the bending moment M1
at the location of U1 degrees of freedom determine the modal static
response
(c) Calculate
and tabulate modal contribution factors their cumulative values for various
numbers of modes included J = 1, 2, 3 and the error ej
for static response. Comment on how the relative values of modal contribution
factors and the error ej are influenced by spatial
distribution of forces.
(d)Determine the peak value of (M1n)0
modal response due to F(t)
Assume td
= 0.598 s which is the same as T1.
The distribution of the pulse td = T1
the fundamental period of the system. For the shock spectrum of half cycle sine
wave Rd = 1.73, 1.14 and 1.06 for T1/td
= 1; T2/td = 0.252; T3/td
= 0.119 respectively. It will be convenient to organize the computation in a
table with following headings: n, Tn/td,
Rdn, M1n and [( M1
n )0 /( p 0 M1st
)]
![]()
(e) Comment
on how the peak modal response determined in part (d) depend on modal static
response, modal contributed factor M1n and Rdn
and S.
(f) Is it
possible to determine the peak value of the total (considering all modes)
response from peak modal response? Justify your answer.
![]()
E = 207.15 GPa m = 33 665 kg
L = 3.81 m
I = 4.1623
├Ś 107
mm4
Step 7 Determine
modal static response as shown in Fig. 18.16. The value of moments due
to forces F is determined by the linear combination to the above three
load cases. The resultants are as given in Table 18.5.
Next we can determine
Step 8 Determine
modal contribution factors, their cumulative values and error.
The modal
contribution factors and error are given in Table 18.6
In the above the modal
contribution factor is largest for first mode and progressively decreases for
the second and third modes.
Step 9 Determine
response to the half cycle sine pulse. The peak modal response equation
is specialized for R = M1 to obtain (see Table 18.7)
Step 10 Comments
ŌĆó For the
given force, the modal response decreases for higher modes. The decrease is
more rapid because of Rdn. It also decreases with mode n.
The peak value of the total
response cannot be determined from the peak modal response because the modal
peaks occur at different time instants. Square root of sum of squares (SRSS)
and complete quadratic combination (CQC) do not apply to pulse excitations.
Program 18.1: MATLAB
program to find the ratio of dynamic shear to static shear in a multi-storey
building
%program
to get modal components of the forces and calculate
%ratio of
dynamic shear to static shear
clc; close all;
% m=45413*[1 0;0 0.5];
m=[1 0 0 0 0;0 1 0 0 0;0 0 1 0
0;0 0 0 1 0;0 0 0 0 1]; disp(ŌĆś mass matrixŌĆÖ)
m
%you can give stiffness matrix disp(ŌĆś stiffness
matrixŌĆÖ)
% k=63600000*[2 -1 ;-1 1];
k=[2 -1 0 0 0;-1 2 -1 0 0;0 -1 2 -1 0;0 0 -1 2
-1;0 0 0 -1 1]; k
a=inv(k);
%or you
can given flexibility matrix directly
%a=[.75 .5
.25;.5 1 .5;.25 .5 .75];
disp(ŌĆś flexibility matrixŌĆÖ) a
c=a*m;
[ms,ns]=size(m);
par=zeros(ns,ns);
%force
vector
%s=[0;500000] s=[0;0;0;-1;2];
su=0;
for i=1:ns su=su+s(i);
end
%imposed
frequency
%omimp=21.376;
disp(ŌĆś imposed frequencyŌĆÖ)
omimp=0.15
%eigen values and eigen vectors
[V,D]=eig(c);
for i=1:ms e(i)=1/D(i,i);
end Qh=max(e)+0.001; Ql=0;
for i=1:ms for j=1:ms
if e(j) > Ql & e(j) < Qh kk=j;
Qh=e(j); else
end end Ql=Qh;
Qh=max(e)+0.001;
om1(i)=e(kk);
omega(i)=sqrt(e(kk)); for l=1:ms
p1(l,i)=V(l,kk); end
end
%Normalizing the mode shape
L=p1'*m*p1;
%develop modal matrix for i=1:ms
for j=1:ms p(i,j)=p1(i,j)/sqrt(L(j,j));
end end
disp(ŌĆś Natural frequencies in
rad/secŌĆÖ) disp(omega)
disp(ŌĆś normalized modal vectorŌĆÖ)
disp(p)
disp(ŌĆś check pT m p=IŌĆÖ) pŌĆÖ*m*p
%for earthquake analysis
%s=[m(1,1);m(2,2);m(3,3);m(4,4);m(5,5)] gamma=pŌĆÖ*s;
for i=1:ns par(i,i)=gamma(i);
end
%modal
contribution of forces
disp(ŌĆś modal contribution of
forcesŌĆÖ) ee=m*p*par
disp(ŌĆś dynamic magnification
factorsŌĆÖ) for i=1:ns
rdn(i,i)=1/(1-(omimp/omega(i))^2);
end
rdn ust=a*ee; u=ust*rdn; for
i=1:ns
dis(i)=0; for j=1:ns
dis(i)=dis(i)+u(i,j); end
end
%disp(ŌĆś amplitude of
displacementsŌĆÖ); dis;
fo=k*disŌĆÖ;
sum=0; for i=1:ns
sum=sum+fo(i); end
ratio=sum/su;
disp(ŌĆś ratio of dynamic base
shear to static shearŌĆÖ) ratio
OUTPUT mass matrix
a =
1.0000 1.0000 1.0000 1.0000 1.0000
1.0000 2.0000 2.0000 2.0000 2.0000
1.0000 2.0000 3.0000 3.0000 3.0000
1.0000 2.0000 3.0000 4.0000 4.0000
1.0000 2.0000 3.0000 4.0000 5.0000
imposed frequency
omimp =
0.1500
Natural frequencies in rad/sec
0.2846 0.8308 1.3097 1.6825 1.9190
normalized modal vector
ŌĆō0.1699 ŌĆō0.4557 ŌĆō0.5969 ŌĆō0.5485 0.3260
ŌĆō0.3260 ŌĆō0.5969 ŌĆō0.1699 0.4557 ŌĆō0.5485
ŌĆō0.4557 ŌĆō0.3260 0.5485 0.1699 0.5969
ŌĆō0.5485 0.1699 0.3260 ŌĆō0.5969 ŌĆō0.4557
ŌĆō0.5969 0.5485 ŌĆō0.4557 0.3260 0.1699
check pT m p=I
ans =
1.0000 ŌĆō0.0000 ŌĆō0.0000 ŌĆō0.0000 0.0000
ŌĆō0.0000 1.0000 0.0000 0.0000 0.0000
ŌĆō0.0000 0.0000 1.0000 0.0000 ŌĆō0.0000
ŌĆō0.0000 0.0000 0.0000 1.0000 ŌĆō0.0000
0.0000 0.0000 ŌĆō0.0000 ŌĆō0.0000 1.0000
modal contribution of forces
ee =
0.1096 ŌĆō0.4225 0.7386 ŌĆō0.6851 0.2594
0.2104 ŌĆō0.5534 0.2102 0.5692 ŌĆō0.4364
0.2941 ŌĆō0.3023 ŌĆō0.6788 0.2122 0.4748
0.3539 0.1575 ŌĆō0.4034 ŌĆō0.7455 ŌĆō0.3625
0.3851 0.5086 0.5640 0.4072 0.1352
dynamic magnification factors
rdn =
1.3845 0 0 0 0
0 1.0337 0 0 0
0 0 1.0133 0 0
0 0 0 1.0080 0
0 0 0 0 1.0061
ratio of dynamic base shear to
static shear
ratio =
1.5039
Related Topics