Modal response of Earthquake analysis of linear systems

Earthquake analysis of linear systems

Usually the systems are idealized as lumped-mass systems. In the first part, we will find the structural response as a function of time when the system is subjected to ground acceleration This is known as the response history analysis (RHA) procedure. In the second part, we can compute peak response of a structure during an earthquake directly from earthquake response or design spectrum without the need for response history analysis. The values given by response spectrum analysis (RSA) are fairly accurate.

1 RHA

Let us assume that earthquake-induced motion u˙˙_g ( t ) is identical to all support points. The equation of motion can be written as

Γ_n is called modal participation factor, implying that it is a measure of the degree to which the nth mode participates in the response. Γ is not independent of how the mode is normalized nor a measure of modal contribution to response quantity.

Modal response

Displacement in physical coordinates may be obtained as

The equivalent static force is the product of two quantities:

•   nth mode contribution;

•   pseudo-acceleration response of the nth mode SDF system.

The nth modal contribution to any response quantity R(t) may be determined by static analysis of structures subjected to external force f_n(t). If R_n^st is the static value

R_n^st may be positive or negative and is independent of how the mode is normalized.

1 Total response

The response contributions of some of the higher modes may under appropriate circumstances be determined by simple static analysis instead of dynamic analysis. For short periods T_n ≤ 1/33

If the period range included is the natural periods from N_d+1 to N, then,

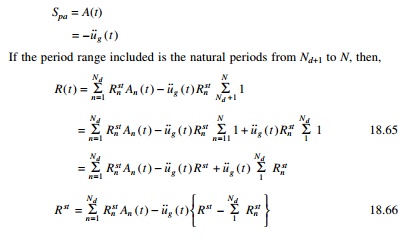
2 Interpretation of modal analysis

At first the dynamic properties natural frequencies and mode shapes of the structure are computed and the force distribution vector mi is expanded into modal components. The rest of the analysis procedure is shown schematically in Table 18.8.

3 Analysis of response to base rotation

The modal analysis procedure is applicable after slight modification when the excitation is base rotation. Consider the cantilever frame shown in Fig. 18.19.

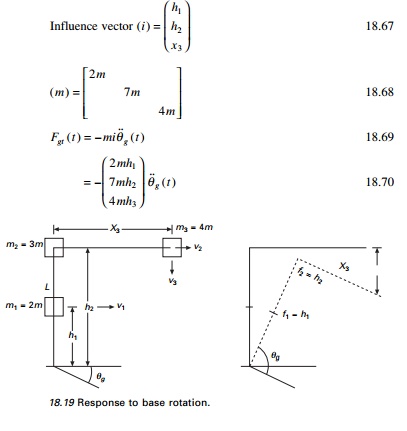
Multi-storey buildings with symmetrical plan

The equation of motion for this structure is (see Fig. 18.20)

Example18.9

The two storey shear frame shown in Fig. 18.21 is excited by a horizontal ground motion u˙˙_g ( t ). Determine

(a)  modal expansion of effective earthquake forces;

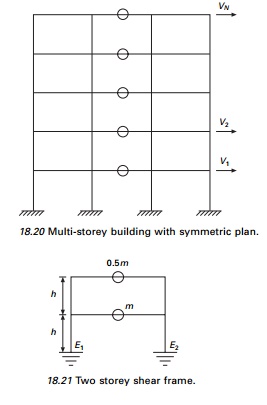
(b) the floor displacement response of D_n(t);

(c)  the storey shear in terms of A_n(t);

(d) the first floor and base overturning moments in terms of A_n(t).

= D₂ ( t ) which is same as [ k ] ^–1( F₂ )ω _n²₂ D₂ ( t ) –.207

Combining we get

u₁(t) = 0.854 D₁(t) + 0.146 D₂ (t) u₂(t) = 1.207 D₁(t) – 0.207 D₂ (t)

(c)  Storey shear can be determined as follows (see Fig. 18.23). Substituting this we get storey shear as

V_b^st  = 1.4565 m A₁ ( t ) + 0.0425 m A₂ ( t )

V₁ (t ) = 0.6035 m A₁ (t ) – 0.1035 m A₂ (t )

(d) Static analysis of the structure for external floor stress F_N gives static responses M _b^st , M₁^st for the overturning moments M_b, and M₁ at the base and first floor respectively.

M_b^st ( t ) = 2.062 mh A₁ ( t ) – 0.062 mh A₂ ( t )

M₁(t) = 0.604 mh A₁(t) – 0.104 mh A₂(t)

Example 18.10

Figure 18.24 shows a two storey frame with flexural rigidity EI for beams and columns (span of the beam = 2h). Determine the dynamic response of the structure to horizontal ground motion u˙˙_g (t ) and express

(a)     floor displacement and joint rotations in terms of Dn (t);       the bending moments in a first storey column and in the second floor

(b)     beam in terms of An(t).

18.12.1 Modal responses

The relative lateral displacement U_in(t) is written as

U_jn(t) = Γ_nϕ_ijD_n(t)

The storey drift is

Dj_n(t) = Uj_n(t) – U_j–1,n(t)

= Γ_n(ϕ_jn – ϕ_j–1, n)D_n(t)

The equivalence static force for the nth mode f_n(t) is given by

f_n(t) = F_nA_n(t)

f_jn(t) = F_jnA_n(t)

where f_jn(t) is lateral force at any jth floor level.

R_n(t) due to nth mode is given by

R_n ( t ) = R_n^st A_n ( t )

The modal static response R_n(st) is determined by static analysis of building due to the external force F_n. The modal static responses are presented in Table 18.9, where

2 Total response

Combining the response contribution of the entire mode gives the earthquake response of the multi-storey building

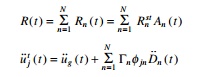
The steps of analysis are given below:

1.     Define ground acceleration u˙˙_g ( t ) numerically at every time step ∆t.

2.     Define structural properties:

(a)  determine mass and stiffness matrix,

(b) estimate modal damping ratio.

3.     Determine natural frequencies (T_n = 2Ï€/ω_n) and natural modes of vibration.

4.     Determine modal components R_N of the effective earthquake force distribution.

5.     Compute the response contribution of nth mode by following steps:

(a)  Perform static analysis of building subjected to F_n forces.

(b) Determine pseudo-acceleration response A_n(t) for the nth mode of SDOF system.

(c)  Determine A_n(t).

6.     Combine modal contributions R_n(t) to determine the total response. As already seen, only lower fewer modes contribute significantly to the response. Hence steps 3, 4 and 5 need to be implemented only for these modes.