Chapter: Civil : Structural dynamics of earthquake engineering
Lumped mass system: shear building
Lumped mass
system: shear building
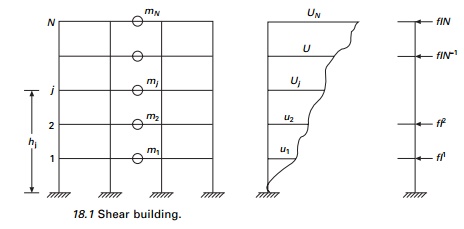
Consider the shear building shown
in Fig. 18.1 subjected to earthquake excitations. The masses of N
stories are lumped at these levels with mj denoting the mass
at the jth floor. The system has n degrees of freedom u1,
u2 ŌĆ” un. Assume there is no damping.
We assume floor displacement
relative to the ground can be expressed as
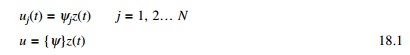
Where z and Žł are the displacement of the roof
and shape function respectively.
Hence total displacement

1 Equation of
motion
Shear Vj in the
jth storey can be given as
Vj
=
kj (storey drift)
= kj
Ōłåj
kj(uj
ŌĆō ujŌĆō1)
kj, the
storey stiffness, is the sum of all lateral stiffness of all columns to that
storey

where EI is the flexural rigidity of the
column and h is the storey height. At each time instant the system is in
equilibrium under the action of
internal storey shear and inertia
force and using DŌĆÖAlembertŌĆÖs principle we get
Using the principle of virtual
displacement to formulate equilibrium equation, the external virtual work can
be written as

The internal virtual work is due
to storey shear Vj(t) acting through storey drifts
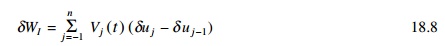
Now we can express displacement
in terms of generalized coordinates as

where Ōłåj, the
stories drift given in terms of storey displacements (see Fig. 18.2), {I}
is a vector with all elements equal to unity. The equations denoted above are
not only applicable to shear building but also to all structures.
Consider a three storey frame
shown in Fig. 18.3. It can be proved,

2 Response
analysis

where h is the height of
the floor above base. In particular the shear and over-turning moment at the
base are
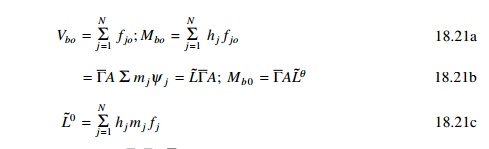
Example 18.1
The uniform five storey shear
frame with rigid beams shown in Fig. 18.4 is subjected to ground acceleration.
All the floor masses are m and all stories have same height and
stiffness k. Assume the displacement to increase linearly with height
above base; formulate the equation of motion for the system and determine
natural frequency.
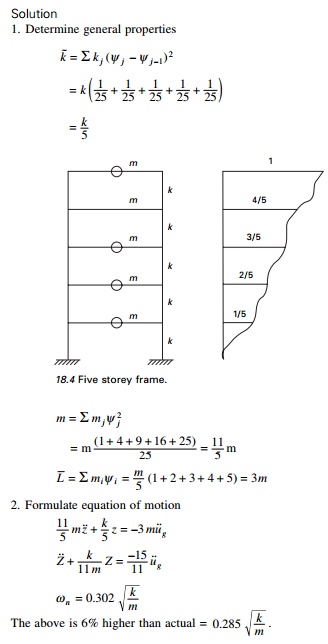
Example 18.2
Determine the peak displacement,
storey shears, floor overturning moment for the above frame with m = 45
412 kg, k = 5530 kN/m; h = 3.657 m due to ground motion
characterized by design spectrum scaled to peak ground acceleration of 0.25g.
The spectrum is given in Fig. 18.5.
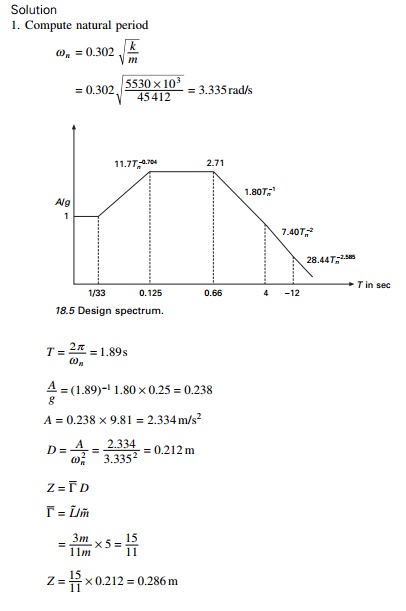
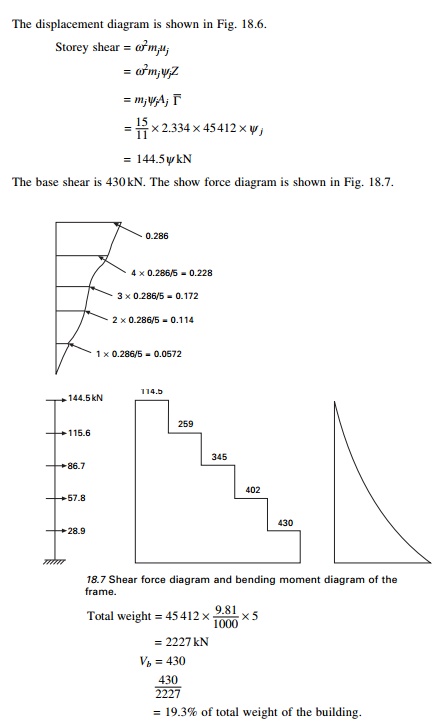
Example 18.3
Solve Example 18.1 using a normalized vector Žå instead of Žł.
The results obtained are the same as the ones
obtained in Example 18.2

Related Topics