Chapter: 11th 12th std standard Class Physics sciense Higher secondary school College Notes
Kepler's laws of planetary motion: The law of orbits, areas, periods
Planetary motion
The ancient
astronomers contributed a great deal by identifying the planets in the solar
system and carefully plotting the variations in their positions of the sky over
the periods of many years. These data eventually led to models and theories of
the solar system.
The first major
theory, called the Geo-centric theory was developed by a Greek astronomer,
Ptolemy. The Earth is considered to be the centre of the universe, around which
all the planets, the moons and the stars revolve in various orbits. The great
Indian Mathematician and astronomer Aryabhat of the 5th century AD stated that
the Earth rotates about its axis. Due to lack of communication between the
scientists of the East and those of West, his observations did not reach the
philosophers of the West.
Nicolaus
Copernicus, a Polish astronomer proposed a new theory called Helio-centric
theory. According to this theory, the Sun is at rest and all the planets move
around the Sun in circular orbits. A Danish astronomer Tycho Brahe made very
accurate observations of the motion of planets and a German astronomer Johannes
Kepler analysed Brahe's observations carefully and proposed the empirical laws
of planetary motion.
Kepler's laws of planetary motion
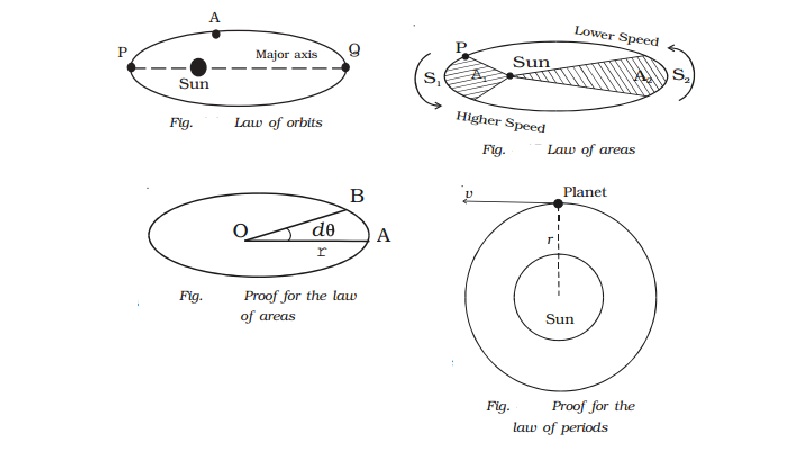
(i) The law of orbits
Each planet moves in an
elliptical orbit with the Sun at one focus. A is a planet revolving round the
Sun. The position P of the planet where it is very close to the Sun is known as
perigee and the position Q of the planet where it is farthest from the Sun is
known as apogee.
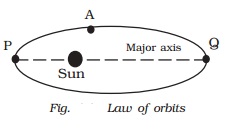
(ii) The law of areas
The line joining the Sun and the
planet (i.e radius vector) sweeps out equal areas in equal interval of times.

The orbit of the planet around
the Sun is as shown in Fig.. The areas A1 and A2 are swept by the radius vector
in equal times. The planet covers unequal distances S1 and S2 in equal time.
This is due to the variable speed of the
planet. When the planet is closest to the Sun, it covers greater distance in a
given time. Hence, the speed is maximum at the closest position. When the
planet is far away from the Sun, it covers lesser distance in the same time.
Hence the speed is minimum at the farthest position.
Proof for the law of areas
Consider a planet moving from A
to B. The radius vector OA sweeps a small angle dθ at the centre in a small
interval of time dt.
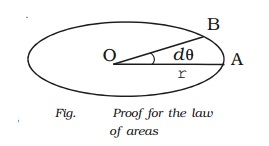
From the Fig., AB = rd θ. The
small area dA swept by the radius is,
dA = ½ x r x rdθ
Dividing by dt on both sides
dA/dt = ½ x r2 x dθ/dt
dA/dt = ½ r2 ω
where ω is the angular velocity.
The angular momentum is given by
L = mr2ω
r2ω = L/m
dA/dt = ½ L/M
Since the line of action of
gravitational force passes through the axis, the external torque is zero.
Hence, the angular momentum isconserved
dA/dt = constant.
(iii) The law of periods
The square of the period of
revolution of a planet around the Sun is directly proportional to the cube of
the mean distance between the
planet and the Sun.
(i.e) T 2 α r3
T 2 / r3 =
constant
Proof for the law of periods
Let us consider a planet P of
mass m moving with the velocity v around the Sun of mass M in a circular orbit
of radius r.
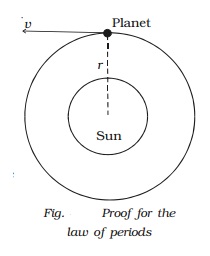
The gravitational force of
attraction of the Sun on the planet is,
F = GMm / r2
The centripetal force is, F = mv2/r
Equating the two forces
Mv2/r = GMm/r2
v2 = GM/r …………….(1)
If T be the period of revolution
of the planet around the Sun, then
v = 2πr /T
Substituting (2) in (1)
R3/T2 = GM
/ 4π2
GM is a constant for any planet
T2 α r3
Related Topics