Comparison of codes for seismic design

Comparison of codes

In all the codes in one way or the other the following parameters are involved.

•       elastic seismic coefficient (base shear);

•       design force reduction;

•       lateral force distribution;

•       overturning moments.

1  Base shear

NEHRP provisions, the source document of the IBC, gives the period formula identical to the Rayleigh method in which static deflection due to a set of lateral forces F_i is u_i assumed as shape function. The period formula given by the NBCC has the same base except that the lateral forces used to determine the static deflections are equal to the lumped weight at the floors. For a linear elastic system we have seen that elastic seismic coefficient C_e is related to pseudo-acceleration spectrum for an SDOF system

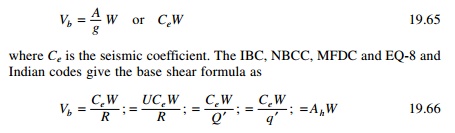
By taking R = Q′ = q′ = 1 C_e in the building code corresponds to A/g and these two values given by Eq. 19.65 and 19.66 are not identical.

2  Design force reduction

Most codes specify that the design base shear to be smaller than the elastic base shear (determined from using elastic seismic coefficient C_e). For most of the codes discussed the reduction factors are R, Q′ and q′ where R = Q′ = q′ = 4 factors independent of T₁ in IBC and NBCC and depends on period in MFDC and EC. The actual strength of the building exceeds design strength, especially for short period systems. The over-strength of a building is usually not recognized explicitly in building codes.

3  Lateral force distribution

According to structural dynamics force at any floor level i

If φ_jn is proportional to h_j then NBCC agrees with structural dynamics formula. Linear mode shape is a reasonable shape for a building in between ρ = 0 and ∞ (ρ = beam to column stiffness). In IBC the height-wise distribution of lateral force based on the assumption that lateral displacement is proportional to the heights when T₁ ≤ 0.5 s and to h ²_j when T₁ ≥ 2.5 s and to an intermediate power of the height for intermediate values of T₁. This is intended to recognize the changing fundamental mode and increasing higher mode contributions to response with increasing T₁. The Indian code uses

but stipulates dynamic analysis for regular buildings h > 40 m in Zones IV and V and h > 90 m in Zones II and III. In such cases

and storey shears for all modes must be done using SRSS and CQC rules.

4  Overturning moments

Certain building codes such as NBC, IBC, and MFDC allow reduction of overturning moment relative to the values computed by lateral force F_j by statics because the response contribution of higher modes are more significant for storey shear than the overturning moments. The reduction factor in IBC at the base of the building varies between 1 (no reduction) and 0.8, depending on the number of stories. The EC-8 permits no reduction of overturning moments relative to the values computed from lateral forces by statics.

In the following, we will calculate shear in various buildings based on IS1893 2002, Part 1. The method used in the other codes will be similar except for some variations. The reader can adapt the following problems according to their country’s seismic code or international building code.