Broad?side on (or) Tan B position - Deflection magnetometer

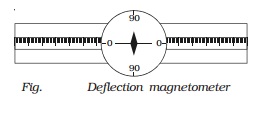
Deflection magnetometer

Deflection magnetometer consists of a small magnetic needle pivoted on a sharp support such that it is free to rotate in a horizontal plane. A light, thin, long aluminium pointer is fixed perpendicular to the magnetic needle. The pointer also rotates along with the needle (Fig.).

There is a circular scale divided into four quadrants and each quadrant is graduated from 0^o to 90^o. A plane mirror fixed below the scale ensures, reading without parallax error, as the image of the pointer is made to coincide exactly with pointer itself. The needle, aluminium pointer and the scale are enclosed in a box with a glass top. There are two arms graduated in centimetre and their zeroes coincide at the centre of the magnetic needle.

Broad?side on (or) Tan B position - Deflection magnetometer

The magnetic field at a point along the equatorial line of a bar magnet is perpendicular to the horizontal component of Earth?s magnetic field. If the magnetometer and a bar magnet are placed in such way that this condition is satisfied, then this arrangement is called Tan B position.

To achieve this, the arms of the deflection magnetometer are placed along the North ? South direction (i.e) along the magnetic meridian. The magnet is placed along East - West direction (i.e) parallel to the aluminium pointer as shown in the Fig..

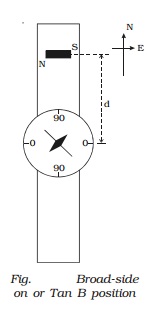
When a bar magnet of magnetic moment M and length 2l is placed at a distance d from the centre of the magnetic needle, the needle gets deflected through an angle θ due to the action of the following two magnetic fields.

(i) The field B due to the bar magnet along its equatorial line

(ii)The horizontal component of Earth?s magnetic field B_h.

The magnetic field at a distance d along the equatorial line of the bar magnet,

B=?₀/4 π  . M/(d²-l²) ^3/2

According to tangent law

B = B_h tan θ

?₀/4 π  . M/(d²-l²) ^3/2 = B_h tan θ

If the magnet is short, l is small compared to d and hence l ² is neglected.

?₀/4 π  . M/d³ = B_h tan θ

Comparison of magnetic moments of two bar magnets

(i) Deflection method

The deflection magnetometer is placed in Tan B position. A bar magnet of magnetic moment M₁ and length 2l ₁ is placed at a distance d₁ from the centre of the magnetic needle, on one side of the compass box (Fig.). Since, the sensitivity of the magnetometer is more at 45^o, the distance

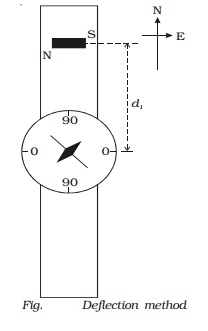
of the bar magnet should be chosen such that the deflection lies between 30^o and 60^o. The readings corresponding to the ends of the aluminium pointer are noted as θ₁ and θ₂. The magnet is reversed pole to pole and kept at the same distance. Two more readings θ₃ and θ₄ are noted. By placing the magnet on the other side of the compass box at the same distance, four more readings θ₅, θ₆, θ₇ and θ₈ are noted as above. The mean of the eight readings gives a value θ_I.

The experiment is repeated as above for the second bar magnet of magnetic moment M₂ and length 2l₂ by placing at a distance d₂. Now the mean of the eight readings gives a value of θ_II.

Applying tangent law, for the first magnet,

?₀/4 π  . M₁/(d₁²-l₁²) ^3/2 = B_h tan θ_I           ????.(1)

and for the second magnet

?₀/4 π  . M₁/(d₂²-l₂²) ^3/2 = B_h tan θ_II           ????.(2)

From the above equations (1) and (2), we get

M₁/M₂ = (d₁²-l₁²) ^3/2 tan θ_{I    /}  (d₂²-l₂²) ^3/2 tan θ_II

Special case

If the magnets are placed at the same distance, then d₁ = d₂ = d

M₁/M₂ = tan θ_I    /  tan θ_II

(ii) Null deflection method

The deflection magnetometer is placed in Tan B position (Fig.). A bar magnet of magnetic moment M₁ and length 2l₁ is placed on one side of the compass box at a distance d₁ from the centre of the magnetic needle. The second bar magnet of magnetic moment M₂ and length 2l₂ is placed on the other side of the compass box such that like poles of the magnets face in the opposite direction. The second magnet is adjusted so that the deflection due to the first magnet is nullified and the aluminium pointer reads 0^o - 0^o. The distance of the second magnet is x₁. The first magnet is reversed pole to pole and placed at the same distance d₁. The second magnet is also reversed and adjusted such that the aluminium pointer reads 0^o - 0^o. The distance of the second magnet is x_2.

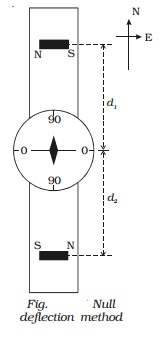
The experiment is repeated by interchanging the magnets. Two more distances x₃ and x₄ are noted. The mean of x₁, x₂, x₃ and x₄ is taken as d₂.

Since the magnetic fields due to the two bar magnets at the centre of the magnetic needle are equal in magnitude but opposite in direction.

B₁ = B₂

M₁/M₂ =  [ (d₁² ? l₁²)² d₂  ] / [ (d₂² ? l₂²)² d₁  ]

M₁/M₂ = (d₁² ? l₁²)^3/2    /   (d₂² ? l₂²)^3/2

If the bar magnets are short, l₁ and l₂ are negligible compared to the distance d₁ and d₂

M₁/M₂ = d₁³ / d₁³