Chapter: 11th 12th std standard Class Physics sciense Higher secondary school College Notes
Bragg's law for X-ray diffraction
Bragg's
law for X-ray diffraction
W.L. Bragg and W.H. Bragg studied the
diffraction of X-rays in detail and used a crystal of rock salt to diffract X-rays
and succeeded in measuring
the wavelength of X-rays.
Consider
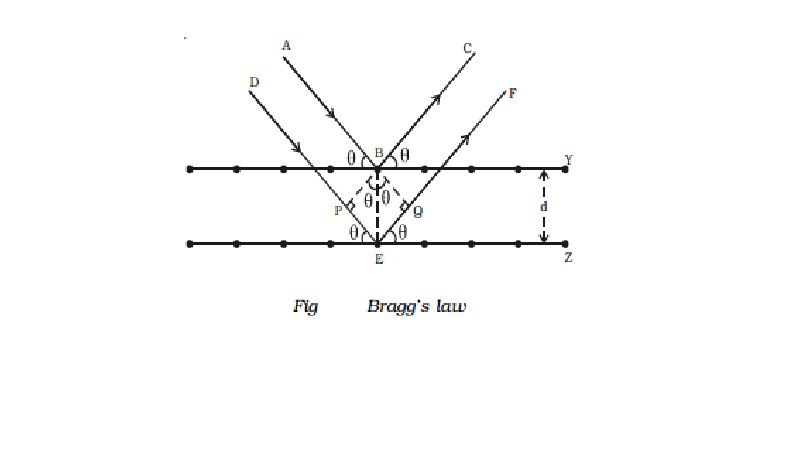
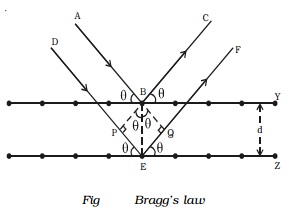
homo-geneous X-rays of wave length λ incident on a crystal at a glancing angle
θ. The incident rays AB and DE after reflection from the lattice planes Y and Z
travel along BC and EF respectively as shown in Fig .
Let
the crystal lattice spacing between the planes be d. BP and
BQ are perpendiculars drawn from B on
DE and EF respectively. Therefore, the path difference between the two
waves ABC and DEF is equal to PE + EQ.
In the ∆PBE, sin θ = PE/BE (or) PE = BE sin θ = d sin θ
In the ∆QBE, sin θ = EQ/BE (or) EQ = BE sin θ = d
sin θ
Path difference = PE + EQ = d sin θ + d
sin θ = 2d sin θ
If this path difference 2d sin θ is equal to integral multiple of wavelength of
X-ray i.e. nλ, then constructive
interference will occur between the reflected beams and they will reinforce
with each other. Therefore the intensity of the reflected beam is maximum.
2d sin θ = nλ where, n
= 1, 2, 3
etc. This is known as Bragg's law.
Related Topics