Angular harmonic oscillator

Angular harmonic oscillator

Simple harmonic motion can also be angular. In this case, the restoring torque required for producing SHM is directly proportional to the angular displacement and is directed towards the mean position.

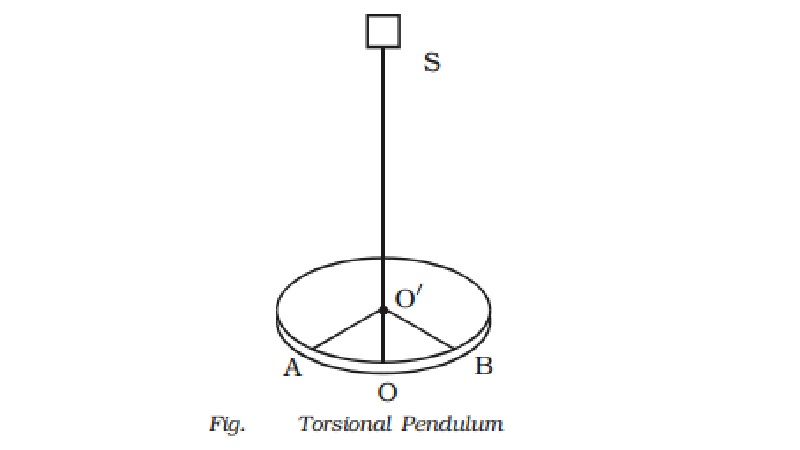
Consider a wire suspended vertically from a rigid support. Let some weight be suspended from the lower end of the wire. When the wire is twisted through an angle θ from the mean position, a restoring torque acts on it tending to return it to the mean position. Here restoring torque is proportional to angular displacement θ.

Hence r = -C θ  ???..(1)

where C is called torque constant.

It is equal to the moment of the couple required to produce unit angular displacement. Its unit is N m rad−1.

The negative sign shows that torque is acting in the opposite direction to the angular displacement. This is the case of angular simple harmonic motion.

Examples : Torsional pendulum, balance wheel of a watch.

But τ = I α ...(2)

where τ is torque, I is the moment of inertia and α is angular acceleration

∴ Angular acceleration,

Α = τ  /I = - C θ / I

This is similar to a = −ω² y

Replacing y by θ, and a by α we get

α = −ω²θ = - (C/I) θ

ω = rt(C/I)

Period of SHM T = 2π rt(I/C)

Frequency  n = 1/T = 1/2 π rt(C/I)