Chapter: 11th 12th std standard Class Physics sciense Higher secondary school College Notes
Addition of vectors: Triangle and Parallelogram law of vectors
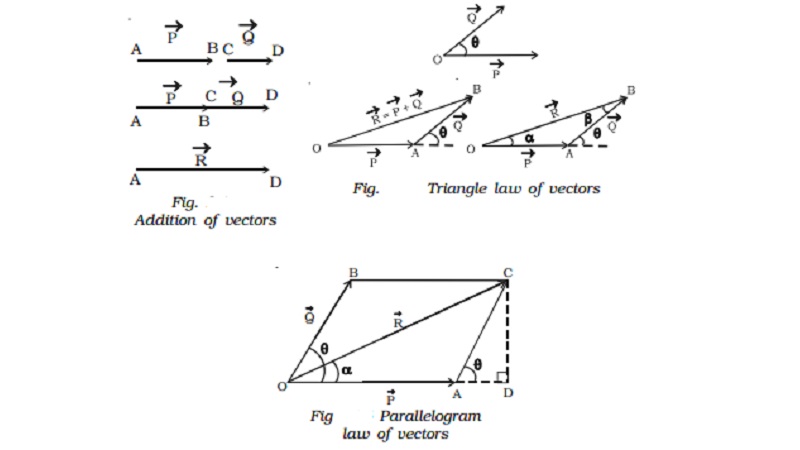
Addition of vectors
As vectors have both magnitude and direction they cannot be added by the method of ordinary algebra.
Vectors can be added graphically or geometrically. We shall now discuss the addition of two vectors graphically using head to tail method.
Consider two vectors Vec P and Vec Q which are acting along the same line. To add these two vectors, join the tail of Vec Q with the head of Vec P (Fig.).
The resultant of Vec P and Vec Q is Vec R = Vec P + Vec Q. The length of the line
AD gives the magnitude of Vec R. Vec R acts in the same direction as that of Vec P and Vec Q.
In order to find the sum of two vectors, which are inclined to each other, triangle law of vectors or parallelogram law of vectors, can be used.
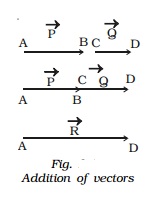
(i) Triangle law of vectors
If two vectors are represented in magnitude and direction by the two adjacent sides of a triangle taken in order, then their resultant is the closing side of the triangle taken in the reverse order.
To find the resultant of two vectors Vec P and Vec Q which are acting at an angle θ, the following procedure is adopted.
First draw O A = JJJG Vec P (Fig.) Then starting from the arrow head of Vec P, draw the
vector = JJJJG JG AB Q . Finally, draw a vector OB = JJJG Vec R from the tail of vector Vec
P to the head of vector Vec Q. Vector = JJJG JG OB R is the sum of the vectors Vec P and Vec
Q. Thus Vec R = Vec P + Vec Q.
The magnitude of Vec P + Vec Q is determined by measuring the length of Vec R and direction by measuring the angle between Vec P and Vec R.

The magnitude and direction of Vec R, can be obtained by using the sine law and cosine law of triangles. Let α be the angle made by the resultant Vec R with Vec P. The magnitude of R is,
R 2 = P 2 + Q 2 - 2PQ cos (180 o - θ)
R = root [ P2 + Q2 + 2PQ cos θ ]
The direction of R can be obtained by
P/ sin β = Q/ sin α = R / sin(1800 - θ)
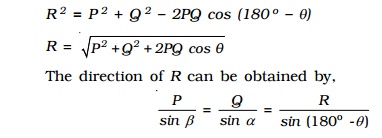
(ii) Parallelogram law of vectors
If two vectors acting at a point are represented in magnitude and direction by the two adjacent sides of a parallelogram, then their resultant is represented in magnitude and direction by the diagonal passing through the common tail of the two vectors.
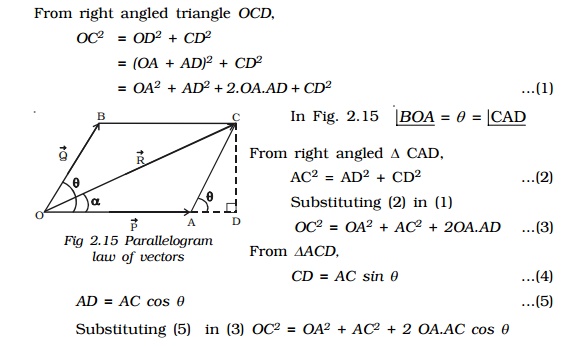
Let us consider two vectors Vec P and Vec Q which are inclined to each other at an angle θ as shown in Fig.. Let the vectors Vec P and Vec Q be represented in magnitude and direction by the two sides OA and OB of a parallelogram OACB. The diagonal OC passing through the common tail O, gives the magnitude and direction of the resultant Vec R.
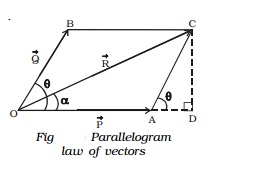
CD is drawn perpendicular to the extended OA, from C. Let COD made by Vec R with Vec P be α.
From right angled triangle OCD,
OC2 = OD2 + CD2
= (OA + AD)2 + CD2
= OA2 + AD2 + 2.OA.AD + CD2 .....(1)
In Fig. Angle BOA = θ =Angle CAD
From right angled ∆ CAD,
AC2 = AD2 + CD2 ...(2)
Substituting (2) in (1)
OC2 = OA2 + AC2 + 2OA.AD ...(3)
From ∆ACD,
CD = AC sin θ ...(4)
AD = AC cos θ ...(5)
Substituting (5) in (3) OC2 = OA2 + AC2 + 2 OA.AC cos θ
Substituting OC = R, OA = P,
OB = AC = Q in the above equation
R2 = P2 + Q2 + 2PQ cos θ
(or)
R = root [ P2 + Q2 + 2PQ cos θ ] ...(6)
Equation (6) gives the magnitude of the resultant. From ∆ OCD,
tan α = CD / OD = CD/( OA +AD )
Substituting (4) and (5) in the above equation,
tan α = ( AC sin θ ) / (OA + AC cos θ )
(or) α = tan-1[Qsin θ / (P+Qcos θ)] ...(7)
Equation (7) gives the direction of the resultant

Special Cases
(i) When two vectors act in the same direction
In this case, the angle between the two vectors θ = 0o, cos 0o = 1, sin 0o= 0
From (6)
R = root [ P2 + Q2 + 2PQ ] = P+Q
From (7)
α = tan-1[Qsin 00 / (P+Qcos 00)]
(i.e) =0

Thus, the resultant vector acts in the same direction as the individual vectors and is equal to the sum of the magnitude of the two vectors.
(ii) When two vectors act in the opposite direction
In this case, the angle between the two vectors θ = 180o, cos 180o = -1, sin 180o = 0.
From (6)
R = root [ P2 + Q2 - 2PQ ] = P-Q
From (7)
α = tan-1[Q / (P-Q)]
(i.e) =0
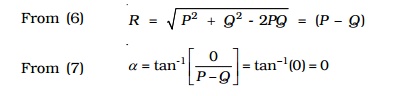
Thus, the resultant vector has a magnitude equal to the difference in magnitude of the two vectors and acts in the direction of the bigger of the two vectors
(iii) When two vectors are at right angles to each other
In this case, θ = 900o , cos 90o = 0, sin 90o = 1
From (6) R=root(P2+Q2)
From (7) a=tan-1(Q/P)
The resultant Vector R vector acts at an angle α with vector Vector P.
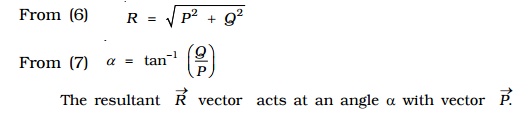
Related Topics