Spectrum analysis by modal response

Spectrum analysis by modal response

In the case of design of structures, complete time history analysis is not necessary; it is enough to valuate the peak values of forces and deformations. A good estimate, although not accurate, of the peak response can be determined directly from response spectrum for the ground motion. These peak modal responses are combined using any one of the rules discussed below to get the value of the total response. This method is known as RSA.

For any response value such as force or deformation, the peak value R_n0 of the nth modal contribution is given by

where A_n(T_n, ρ_n) is the ordinate of the pseudo-acceleration response spectrum corresponding to the natural vibration period T_n = 2π/ω and the damping ratio ρ_n. R_n0 is either positive or negative depending on whether R_n^st is positive or negative.

1 Modal contribution rules

Knowing the peak value R_n0 of the nth mode contribution it is necessary to find the peak value R₀ if the total response R(t). As we have seen in earlier chapters, the peak value R_n0 for each node occurs at different times and the combined peak response may attain its peak at a different time instance.

2 Absolute sum rule

If we assume that all peak values of modal responses occur at the same time, and ignore the algebraic sign for the peak value of the total response, we get

The above estimate is highly conservative and not popular in structural design applications.

3 SRSS rule

The SRSS rule provides an estimate of peak value according to the equation

The algebraic sign of R_n0 does not affect the value of R₀. This rule is applicable for structures where natural vibration frequencies are well separated. The SRSS rule was developed by Rosenblueth (1951).

4 CQC rule

The rule is applicable to wide range of structures in which natural frequencies of closely spaced such as those in unsymmetric buildings. According to the CQC rule (first developed by Rosenblueth and Elorduy)

It is assumed that the damping ratio ς is the same for all modes. Figure 18.27 shows the variation of correlation coefficient with respect to β_ij. It is to be observed that the correlation coefficient ρ_ij is significant at β_ij = 1.

In ρ matrix the leading diagonal terms are equal to 1. Hence Eq. 18.78 is rewritten as

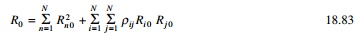
The first summation of the right-hand side is identical to SRSS combination rule, whereas the next term may be positive or negative, depending the algebraic signs of R_n0. It is also seen from Fig. 18.27 that ρ_ij ≈ 0 when ω_i, ω_j move farther apart. For well-separated vibration frequencies ρ_ij vanish. As a result the second term can be neglected and Eq. 18.83 reduces to the SRSS rule.

5 Factors influencing the earthquake response

There are two parameters which influence the earthquake response: (1) fundamental natural vibration period T₁ and (2) beam to column stiffness ratios based on the properties of the beam and column in the storey closest to the mid-height of the frame.

where EI_b and EI_c are the flexural rigidities of beams and columns and L_b and L_c denote the lengths of the beams and columns. If γ → ∞ the beam imposes no restraint on joint rotations and the frame will bend as a flexure beam. If λ > ∞ the structure will behave like a shear beam with double curvature bending in each column. An intermediate value of γ represents the column and beam undergoing double curvature bending. This property γ controls several properties of the structure when γ is small and the vibration periods are more separated.

As the fundamental period increases with the velocity and displacement-sensitive regions of the structure, the higher mode response generally becomes an increasing percentage of the total response. For design accuracy more modes should be included in the analysis of buildings with longer periods than the buildings with shorter period. More modes should be included in the analysis of buildings with smaller γ. In some codal provisions, we have to include the number of modes such that 90% of the total mass is the participating mass.