Effective modal mass and modal height

Effective modal mass and modal height

The base shear for ‘n’ mode is calculated as

M _n^* is called base shear modal mass or brevity effective modal mass. From that it is clear that only the portion of M_n of the mass of a multi-storey building is effective in producing base shear due to nth mode because the building mass is distributed among various floor levels and the equivalent static force m_jϕ_jn varies over the height. The sum of effective modal masses M_n over the modes is equal to the mass of this building.

Example 18.11

Determine the effective modal mass and the effective modal height for the frame shown in Fig. 18.29.

Solution

The modal distribution of effective earthquake force is given in Fig. 18.30. Taking moment at base

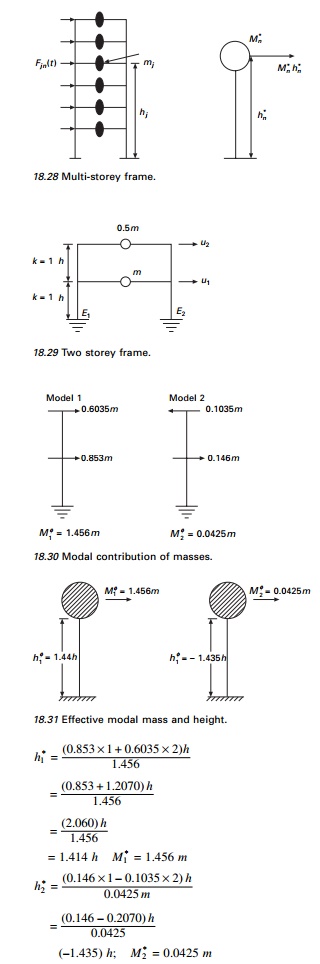
The effective modal mass and modal height are indicated in Fig. 18.31.

Example 18.12

Consider a five storey building (Example 18.1) (see Fig. 18.32) whose properties are given. Calculate effective modal mass and height.

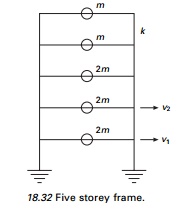
The effective modal mass and modal height are shown in Fig. 18.34.

The ground acceleration u˙˙_g (t ) is defined by its numerical value as time instant equally spaced at ∆t. This time step is chosen small enough to define u˙˙_g ( t ) and to determine accurately the response of the SDOF system:

Base shear = m (7.0926A₁(t) + 0.6471A₂(t) + 0.2A₃(t)

+ 0.0528A₄(t) + 0.0003A₅(t))

Base moment = mh (7.0927 × 3.079A₁(t) + 0.6471 × (–1.563)A₂(t)

+ 0.2A₃(t) + 0.0528 × (–0.587)A₄(t)

0.0003 × 7.67A₅(t))

Multiple support excitation

There are certain examples in which the ground motion generated by an earthquake is different from support to support. For example the Golden Gate Bridge is 1965 m in length and the ground motion is expected to vary significantly over the length of the base at the two ends of the bridge.

Example18.13

A uniform two span continuous bridge shown in Fig. 18.35 with flexural stiffness EI idealized as lumped mass. Let us formulate the equation of motion subjected to vertical motion at 1, 2, 3 as u_g1, u_g2, u_g3 at supports.

Formulation stiffness matrix 10 × 10. Assuming translational displacement as master and other degrees of freedom as slaves we get reduced stiffness matrix of size 5 × 5.

 Apply unit load at 3 (to get influence vector i₁)

Moment at 4 = L

Calculate u₂ when u₃ = 1

The – sign shown the deflection at 2 is downward.

Now calculate deflection at 1 due to unit load at 3= deflection at 3 due to unit load at 1.

Apply unit load at 1

Both deflections at 3 and 1 are upwards and hence positive. If u₃ = 1 let us calculate what is u₁. 

To find the influence vector i₂, apply unit load at 4 and find the deflection at 1 and 4. The deflection at 4 due to unit load at 4 is given by L³/6EI. If the load is at a distance of ×2 and the deflection is to be calculated at ×1, then deflection at ×1 is given

When the deflection at 4 is equal to 1 what is the deflection at 1 and 2 which may be calculated as

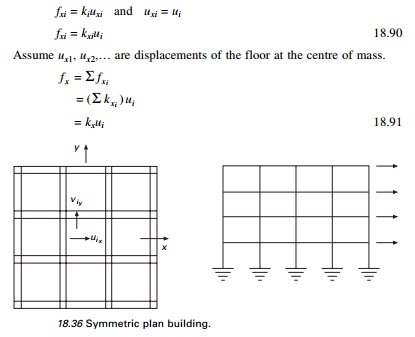
Symmetric plan buildings: translational ground motion

Consider an N-storey symmetric plan building having rigid floor displacement and several frames in each x and y direction as shown in Fig. 18.36.

1 One storey, two way unsymmetric system

Consider the idealized one storey frame shown in Fig. 18.37. Assume the diaphragm is rigid. Assume frame A is located at a distance of e:

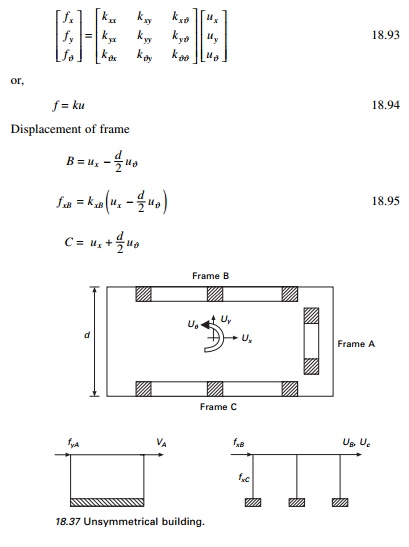
2 Equation of motion

Considering earthquake excitation defined by u˙˙_gx ( t ), u˙˙_gy ( t ), u˙˙_gθ ( t ) , we get the equation of motion if (k_xC = k_xB)

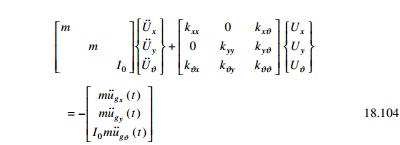
The above equations are coupled. Thus the response of the system to x and y components of ground motion is not restricted to lateral displacement x and y directions but will also include lateral motions in tranverse directions and the torsion of the roof diaphragm about the vertical axis.

In Fig. 18.36, if frame A passes through the centre of mass ‘O’, then (e = 0) (k_xB = k_xC).

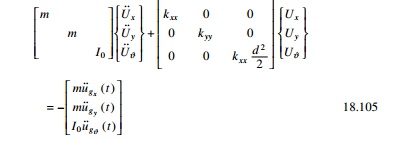
All three equations are uncoupled and solved.