Chapter: 11th 12th std standard Class Physics sciense Higher secondary school College Notes
Motion of a projectile projected at an angle with the horizontal (oblique projection)
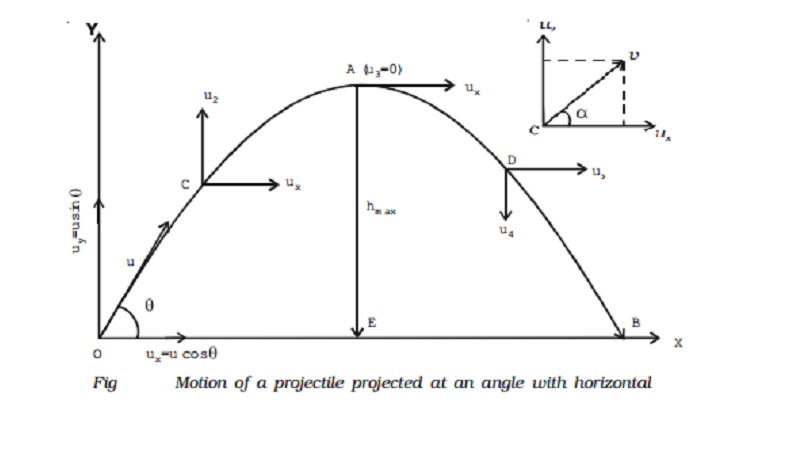
Motion of a projectile projected at an angle with the horizontal (oblique projection)
Consider a body projected from a point O on the surface of the Earth with an initial velocity u at an angle θ with the horizontal as shown in Fig.. The velocity u can be resolved into two components
ux = u cos θ , along the horizontal direction OX and
uy = u sin θ, along the vertical direction OY
The horizontal velocity ux of the object shall remain constant as no acceleration is acting in the horizontal direction. But the vertical component uy of the object continuously decreases due to the effect of the gravity and it becomes zero when the body is at the highest point of its path. After this, the vertical component uy is directed downwards and increases with time till the body strikes the ground atB.
Path of the projectile
Let t1 be the time taken by the projectile to reach the point C from the instant of projection.
Horizontal distance travelled by the projectile in time t1 is,
x = horizontal velocity x time
x = u cos θ x t1 (or) t1 = x / u cos θ ... (1)
Let the vertical distance travelled by the projectile in time t1 = s = y
At O, initial vertical velocity u1= u sin θ From the equation of motion
s = u1 t1 - 1/2 gt12
Substituting the known values,
y = (u sin θ) t1 - 1/2 gt12 ..(2)
Substituting equation (1) in equation (2),
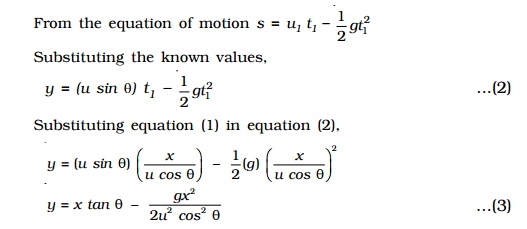
The above equation is of the form y = Ax + Bx2 and represents a parabola. Thus the path of a projectile is a parabola.
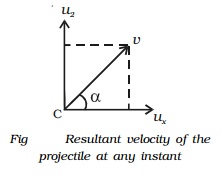
Resultant velocity of the projectile at any instant t1
At C, the velocity along the horizontal direction is ux = u cos θ and the velocity along the vertical direction is uy= u2.
From the equation of motion,
u2 = u1 - gt1
u2 = u sin θ - gt1
∴ The resultant velocity at
C is v=root[ux2+u22]
v=root[(ucos θ)2 + (u sin θ-gt1)2]
=root[u2+g2t21-2ut1gsin θ]
The direction of v is given by
tan α =u2/ux = [ u sin θ- gt1 ] / [ u cos θ]

where α is the angle made by v with the horizontal line.
Maximum height reached by the projectile
The maximum vertical displacement produced by the projectile is known as the maximum height reached by the projectile. In Fig,EA is the maximum height attained by the projectile. It is represented as hmax.

At O, the initial vertical velocity (u1) = u sin θ
At A, the final vertical velocity (u3) = 0
The vertical distance travelled by the object = sy = hmax
From equation of motion, u32 = u21 - 2gsy
Substituting the known values, (0) 2= (u sinθ) 2 - 2ghmax
2ghmax = (u sinθ) 2
hmax = (u sinθ) 2 / 2g
Time taken to attain maximum height
Let t be the time taken by the projectile to attain its maximum height.
From equation of motion u3 = u1 - g t
Substituting the known values 0 = u sin θ - g t
g t = u sin θ
t = (u sin θ) / g
Time of flight
Let tf be the time of flight (i.e) the time taken by the projectile to reach B from O through A. When the body returns to the ground, the net vertical displacement made by the projectile

(i.e) the time of flight is twice the time taken to attain the maximum height.
Horizontal range
The horizontal distance OB is called the range of the projectile. Horizontal range = horizontal velocity x time of flight
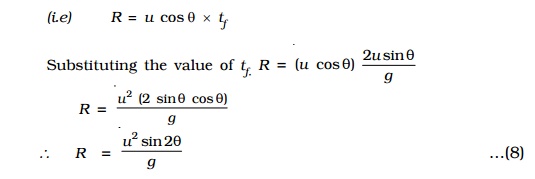
(i.e) R = u cos θ x tf
R = u 2 (2 sinθ cosθ) / g
R = (u 22 sin2θ)/g
Maximum Range
From (8), it is seen that for the given velocity of projection, the horizontal range depends on the angle of projection only. The range is maximum only if the value of sin 2θ is maximum.
For maximum range Rmax sin 2θ = 1
(i.e) θ = 45
Therefore the range is maximum when is 45o.
Therefore the range is maximum when the angle of projection is 45o.
Rmax =( u2 x 1) /g
Rmax = u2 /g
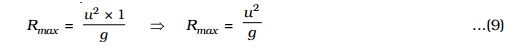
Related Topics