Important terms in simple harmonic motion

Important terms in simple harmonic motion

(i) Time period

The time taken by a particle to complete one oscillation is called the time period T.

In the Fig., as the particle P completes one revolution with angular velocity ω, the foot of the perpendicular N drawn to the vertical diameter completes one vibration. Hence T is the time period .

Then ω = 2 π/T  or T = 2π / ω

The displacement of a particle executing simple harmonic motion may be expressed as

y(t) = a sin ( 2 π / T ) t ...(1)

 and y(t) = a cos ( 2 π/T )  t ...(2)

 where T represents the time period, a represents maximum displacement (amplitude).

 These functions repeat when t is replaced by (t + T).

 y (t + T) = a sin [2 π/T (t + T) ]...(3)

  = a sin [2 π t/ T + 2 π ]

= a sin ( 2 π  t/ T )   = y (t)

 In general y (t + nT) = y (t )

Above functions are examples of periodic function with time period T. It is clear that the motion repeats after a time T = 2π / ω where ω is the angular frequency of the motion. In one revolution, the angle covered by a particle is 2π in time T.

ii. Frequency and angular frequency

The number of oscillations produced by the body in one second is known as frequency. It is represented by n. The time period to complete one oscillation is 1 / n .

 T = 1 n shows the time period is the reciprocal of the frequency. Its unit is hertz. ω = 2π n, is called as angular frequency. It is expressed in rad s⁻¹.

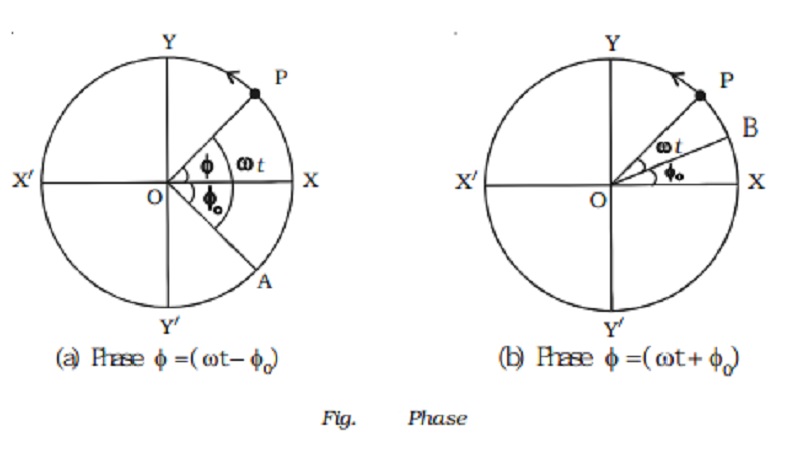
iii. Phase

The phase of a particle vibrating in SHM is the state of the particle as regards to its direction of motion and position at any instant of time. In the equation y = a sin (ωt + φ_o) the term (ωt + φ_o) = φ, is known as the phase of the vibrating particle.

Epoch

It is the initial phase of the vibrating particle (i.e) phase at t = 0. ∴ φ = φo (∵ φ = ωt + φo) The phase of a vibrating particle changes with time but the epoch is phase constant.

1.If the particle P starts from the position X, the phase of the particle is Zero.

2.Instead of counting the time from the instant the particle is at X, it is counted from the instant when the reference particle is at A (Fig. a) . Then ang XO P = (ωt − φ_o).

Here (ωt − φ_o) = φ is called the phase of the vibrating particle. (−φ_o) is initial phase or epoch.

3.If the time is counted from the instant the particle P is above X (i.e) at B, [Fig. b] then (ωt + φo) = φ. Here (+φo) is the initial phase.

Phase difference

If two vibrating particles executing SHM with same time period, cross their respective mean positions at the same time in the same direction, they are said to be in phase.

If the two vibrating particles cross their respective mean position at the same time but in the opposite direction, they are said to be out of phase (i.e they have a phase difference of π).

If the vibrating motions are represented by equations

y₁ = a sin ωt and

 y₂ = a sin (ωt − φ) 

then the phase difference between their phase angles is equal to the phase difference between the two motions.

∴ phase difference = ωt − φ − ωt = −φ negative sign indicates that the second motion lags behind the first.

If y2 = a sin (ωt + φ),

phase difference = ωt + φ − ωt = φ

Here the second motion leads the first motion.

We have discussed the SHM without taking into account the cause of the motion which can be a force (linear SHM) or a torque (angular SHM).

Some examples of SHM

1.     Horizontal and vertical oscillations of a loaded spring.

2.     Vertical oscillation of water in a U−tube

3.     Oscillations of a floating cylinder

4.     Oscillations of a simple pendulum

5.     Vibrations of the prongs of a tuning fork.