How the response spectrum is constructed

How the response spectrum is constructed

Assume for any earthquake ground motion record u˙˙_g (t ) is available.

1.     Numerically define the ground acceleration u˙˙_g ( t ) coordinates at every 0.02 s.

2.     Select natural vibration period and damping factor ρ for a SDOF system.

3.     Compute the deformation response u(t) of the SDOF system to the ground motion u˙˙_g ( t ) by any of the numerical methods discussed in previous pages.

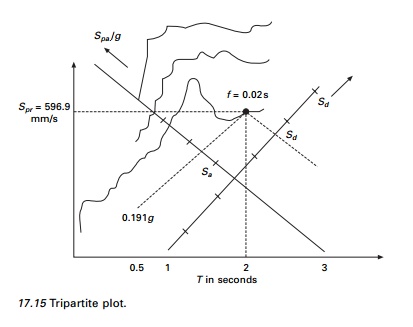
4.     Determine u_max peak value of u(t).

5.     S_d = u_max; S_pv = (2π/T_n) S_d; S_pa = (2π/T_n)² S_d.

6.     Repeat steps 2 to 5 for a range of T_n and ρ covering all the possible systems of engineering interest.

7.     Present these results as three different spectra or all spectra on one sheet.

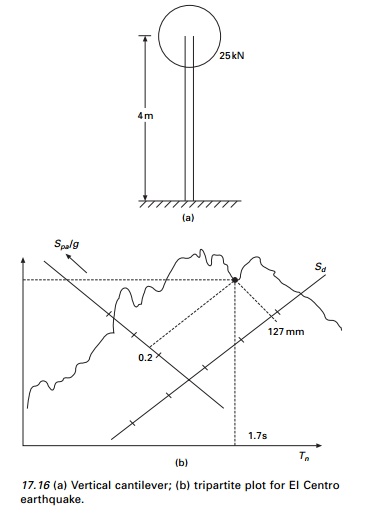
Example 17.3

A 4 m long vertical cantilever 100 mm internal diameter steel pipe supports 25 kN weight attached on the top as shown in Fig. 17.16a. D_o = 115 mm, D_i = 100 mm, I = 3.676 × 10⁶ mm ⁴ E = 200 × 10⁶ kN/m². Determine the peak deflection; bending stress due to El, Centro ground motion.

₌ [ 3 × 200 × 10 ⁶ × 10 ³ × 3.676 × 10 ^–6   ]/  64

= 34.46 × 10³ N/m

Total weight of the pipe (weight /m = 0.01875 kN/m) = 0.01875 × 4 = 0.075 kN Compared with the top weight, the pipe weight is very small and can be

neglected.

W = 25 kN

= 25 000 N

The stress calculation exceeded the limit, hence the designer decided to increase the size of the pipe as D₀ = 220 mm; D_i = 200 mm; I = 3.645 × 10⁷ mm⁴. Comment on the advantage or disadvantage of using bigger pipes.

k = 3EI/l³

k = 341.71 kN/mm

m = 2548 kg

The above example points out an important difference between the response of structures due to earthquake excitation and a fixed value of static force. In the static case, the stress decreases by increasing the size of the member. In the case of earthquake excitation the increase in frequency shortens the natural period from 1.7 to 0.54 s which for this spectrum increases the inertia force. Increase or decrease in stress depends on section modulus.

Example 17.4

A single storey reinforced concrete (RC) building (see Fig. 17.17a) is idealized for this purpose of structural analysis as a mass-less frame supporting a dead load (DL) of 50 kN on the beam level. The frame is 8 m wide and 4 m high. Each column and beam have a 250 mm square section. Assuming ρ = 5%, determine peak response of the frame due to El Centro ground motion. In particular determine the peak lateral deflection at the beam level and plot the diagram of bending moment at the instant of peak response.

Solution

I = ₁₂¹ × 250 ⁴  = 3.256 × 10⁸ mm ⁴ ; E = 30 × 10 ⁶ kN/m ²

The beam is not rigid. The stiffness of the beam has to be taken into account.

ρ = 0.05 s_pa = 0.76g s_d = 17 mm (read from spectrum) static force = m a = 50 × 0.76 = 38 kN

Consider half of the frame due to symmetry

Stiffness of beam = 6I/L = 6/8 = 0.75 (for Nylor’s moment distribution)

Stiffness of column = I/h = ¹/4 =0.25

Sway moment at top and bottom = 19 × 2 = 38 kN/m

Moment distribution for half of the frame is shown in Fig. 17.17b and the bending moment diagram is shown in Fig. 17.17c.

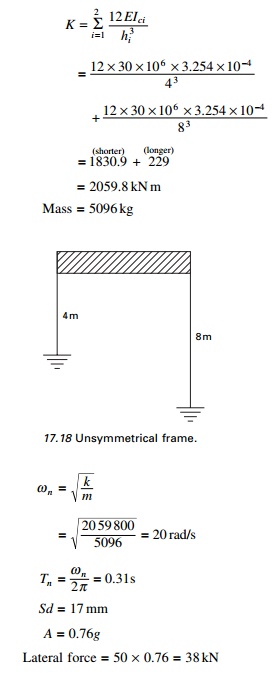
Example 17.5

The frame shown in Fig. 17.18 is for use in a building to be located on sloping ground. The beams are made much stiffer than columns and can be assumed to be rigid. The cross-section of the columns is 250 mm square but their lengths are 4 m and 8 m respectively. Determine the base shear in the two columns, at the instant of peak response due to El Centro ground motion. Assume damping as 5% of critical damping.

Solution

Since the beam is rigid, the stiffness of columns can be taken as

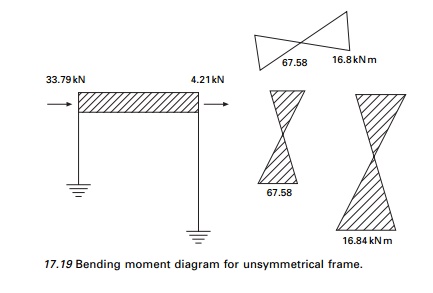
Force shared by long column = 38 – 33.79 = 4.21 kN

The shear in columns as well as bending moment diagram are shown in Fig. 17.19.

Observe that both columns go through equal deflection. The stiffer column carries greater force than the flexible column. Sometimes this basic principle is not recognized in building design, leading to unanticipated damage to the stiffer structure.