Velestos and Newmark spectra

Combined deformation, velocity and acceleration (DVA) spectrum

Each of the deformation pseudo-velocity and pseudo-acceleration response spectra for given ground motion contains the same information, no more no less. The three different spectra are simply different ways of presenting the same information on the structural response. Knowing one of the spectra, the other two can be obtained by algebraic operation.

Then why do we need three spectra? Each one gives different physical meanings. The deformation spectrum directly provides peak deformation of the system. The pseudo-velocity spectrum gives peak strain energy stored in the system. The pseudo-acceleration spectrum is related directly to the peak value of the equivalent static force and base shear. For this purpose a combined plot showing all three of the spectral quantities is especially useful. This type of plot was developed by A S Velestos and N M Newmark in 1960 for earthquake response.

Velestos and Newmark spectra

The relationship between pseudo-spectral acceleration, pseudo-spectral velocity and spectral displacement may be written as (shown in Fig. 17.14)

The curve between log S_pv and log T_n is a straight line with +45° slope for which S_pa is constant. Hence the slope of log S_pa is –45°.

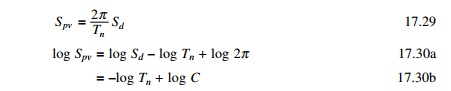
Hence log S_pv vs. log T_n line is a straight line with – ve slope of 45°. Hence S_d line is constant at an angle of +45°.

Once the graph paper has been constructed, the three responses of deformation, pseudo-velocity and pseudo-acceleration of Fig. 17.15 can readily be combined into one plot. For example V = 596.9 mm/s for T_n = 2 s is plotted and the corresponding S_d = 189.7 mm and S_pa = 0.191g is read from the graph. The four-way plot is a complete presentation of deformation, pseudo-velocity and pseudo-acceleration plots.

A response spectrum should cover a wide range of natural periods and several damping values so that it provides a peak response for all possible structures. The period range should be extended because tall buildings and long bridges may have longer vibration periods and several damping ratios will need to be included from 0 to 20% over a period range of 0.2 to 50 s. The response spectrum has proved to be very useful in earthquake engineering for all ground motions.