Generation of sinusoidal waves by a tuned LC circuit

Generation of sinusoidal waves by a tuned LC circuit

Sinusoidal oscillators consist of two main sections : a frequency determining device and maintaining device. A resonant LC network can be used as frequency determining device. The frequency maintaining device is a transistor amplifier with its power supply. The amplifier must have sufficient gain to compensate for the attenuation of the frequency determining section and must introduce required phase shift for positive feedback.

If a capacitor of capacitance C and an inductor of inductance L are connected in parallel, then such a circuit represents an oscillatory circuit.

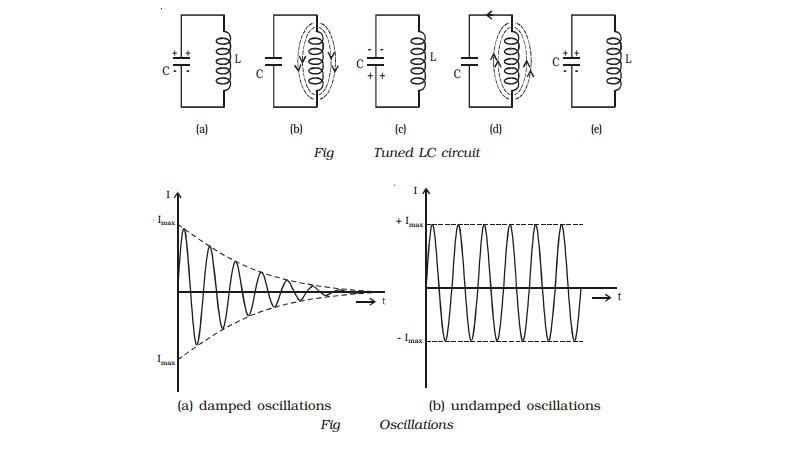
Let us consider a fully charged capacitor C connected with an inductance L as shown in Fig a. When the charged capacitor is connected to inductance L, the capacitor will discharge, sending current through L and induce magnetic field as shown in Fig b. Thus the electrostatic energy stored in the capacitor has been converted into electromagnetic energy associated with inductance L.

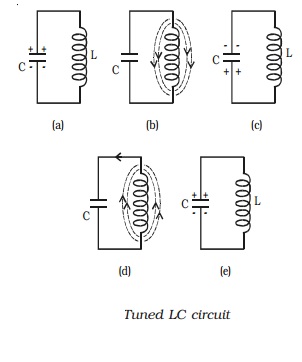
When the capacitor is completely discharged, the induced magnetic field begins to collapse, sending current in the same direction. The capacitor C is now charged with opposite polarity (Fig c). In this case, energy associated with magnetic field is converted into electrostatic energy. This energy is stored in the capacitor. Once the capacitor is completely charged, it begins to discharge in the reverse direction producing again a magnetic field across L in the opposite direction (Fig d). Again the magnetic field will collapse and will charge the capacitor. The circuit returns to the original state. (Fig e). This charging and discharging process results in oscillating current and hence electrical oscillations are set up in the LC circuit. When a LC circuit is used to store energy, it is called tank circuit. The frequency of oscillations is given by,

 f= 1/ 2π/rt(LC)

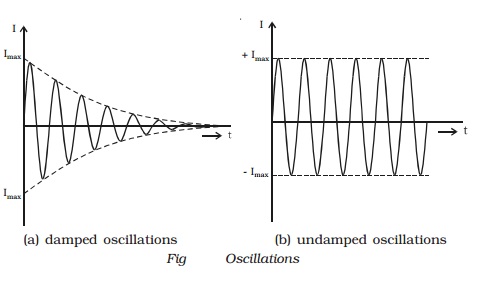
If there are no power losses in the LC circuit, then the electrical oscillations will continue for indefinite time. But, in practice, there is some power loss during each cycle of oscillation, as some resistance is always associated with a given LC circuit. Hence the amplitude of oscillations decreases gradually and becomes zero, when all the energy is consumed as losses. Therefore, damped oscillations are produced in the circuit (Fig a). I_max represents the maximum current flowing through the circuit.