Definition, Geometrical representation, Properties, Proof, Solved Example Problems - Conjugate of a Complex Number | 12th Mathematics : UNIT 2 : Complex Numbers
Chapter: 12th Mathematics : UNIT 2 : Complex Numbers
Conjugate of a Complex Number
Conjugate of a Complex
Number
In this section, we study about conjugate of a complex number,
its geometric representation, and properties with suitable examples.
Definition 2.3
The conjugate of the complex number x + iy is
defined as the complex number x ŌłÆ i y.
The complex conjugate of z is denoted by ![]() .
To get the conjugate of the complex number z , simply change i by
ŌłÆi in z. For
instance 2 ŌłÆ 5i is the
conjugate of 2 + 5i. The product of a complex number with its conjugate is
a real number.
.
To get the conjugate of the complex number z , simply change i by
ŌłÆi in z. For
instance 2 ŌłÆ 5i is the
conjugate of 2 + 5i. The product of a complex number with its conjugate is
a real number.
For instance, (i) (x+iy)( x+iy) = x2 ŌĆō (iy) = x2+y2
(ii) (1 + 3i)(1-3i) = (1)2 ŌĆō (3i)2 = 1 + 9 =10.
Geometrically, the conjugate of z is obtained by
reflecting z on the real axis.
1. Geometrical representation of conjugate of a complex number
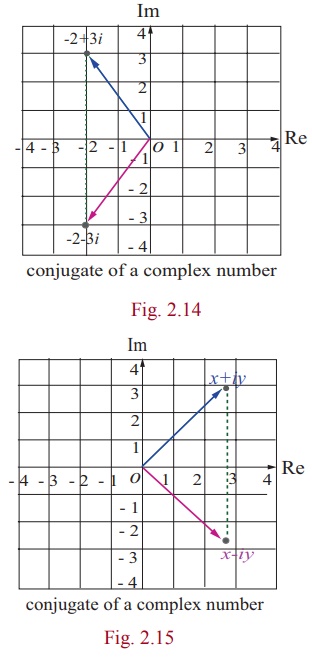
Two complex numbers x+iy and x-iy
are conjugates to each other. The conjugate is useful in division of complex
numbers. The complex number can be replaced with a real number in the
denominator by multiplying the numerator and denominator by the conjugate of
the denominator. This process is similar to rationalising the denominator to
remove surds.
2. Properties of Complex Conjugates
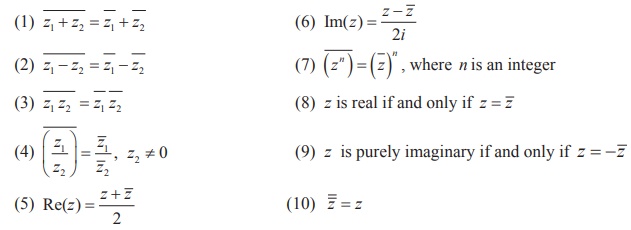
Let us verify some of the properties.
Property
For any two complex numbers z1 and z2, we have 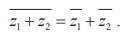 .
.
Proof
Let z1 = x1 + iy1 , z2 = x2 + iy2 , and x1 , x2 , y1 , and y2 Ōłł R
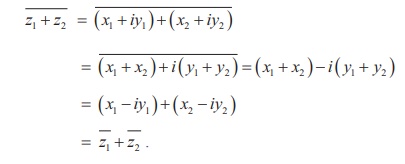
It can be generalized by means of mathematical induction to sums
involving any finite number of terms 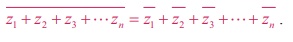
Property
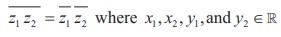
Proof
Let z1 = x1 + iy1 and z2 = x2 + iy2.
Then, z1z2 = ( x1 + iy1 )( x2 + iy2 ) = ( x1 x2 - y1 y2 ) + i ( x1 y2 + x2 y1 ) .
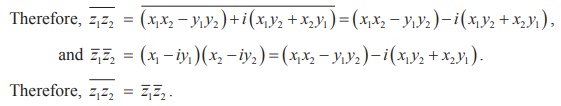
Property
A complex number z is purely imaginary if and only if z
= ŌłÆ ![]()
Proof
Let z = x i + y . Then by definition ![]() = x ŌłÆ iy
= x ŌłÆ iy
Therefore, z = ŌłÆ![]()
Ōćö x + iy =
ŌłÆ (x ŌłÆ iy)
Ōćö 2x = 0 Ōćö
x = 0
Ōćö z is purely imaginary.
Similarly, we can verify the other properties of conjugate of
complex numbers.
Example 2.3
Write 3+4i / 5-12i in the xi + y form, hence
find its real and imaginary parts.
Solution
To find the real and imaginary parts of [3+4i] / [5-12i]
, first it should be expressed in the rectangular form x + iy. To
simplify the quotient of two complex numbers, multiply the numerator and
denominator by the conjugate of the denominator to eliminate i in the
denominator.
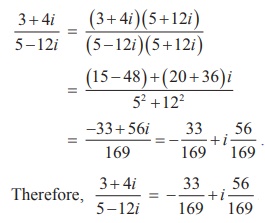
This is in the x + iy form.
Hence real part is ŌĆō 33/169 and imaginary part is 56/169
Example 2.4
Simplify 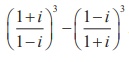 into rectangular form
into rectangular form
Solution
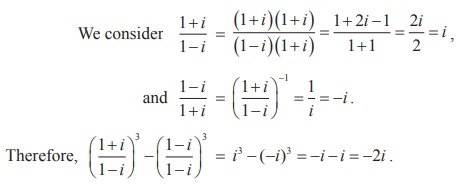
Example 2.5
If 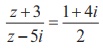 , find the complex number z in the rectangular
form
, find the complex number z in the rectangular
form
Solution
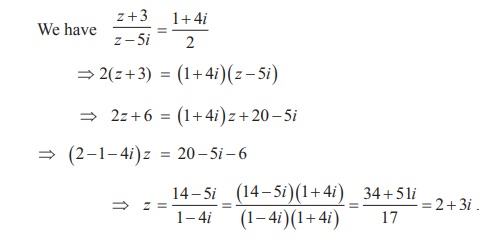
Example 2.6
If z1 = 3 ŌłÆ 2i and z2 = 6 + 4i , find z1/z2 in the rectangular
form
Solution
Using the given value for z1 and z2 the value of z1/z2 =
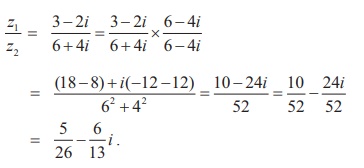
Example 2.7
Find zŌłÆ1, if z = (2+3i) (1ŌłÆ i).
Solution
We have z = (2 + 3i )(1- i ) = (2 + 3) + (3
- 2)i = 5 + i
ŌćÆ z-1 = 1/ z = 1/[5 + i ].
Multiplying the numerator and denominator by the conjugate of
the denominator, we get
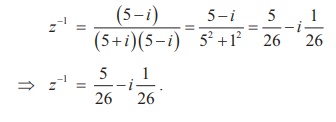
Example 2.8
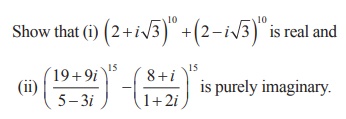
Solution
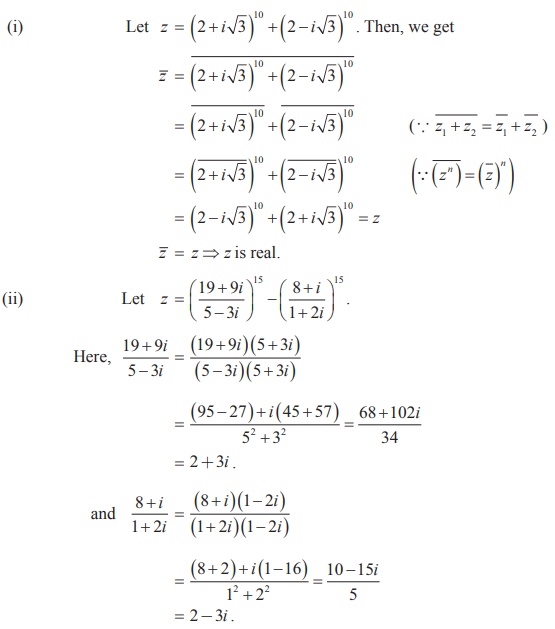
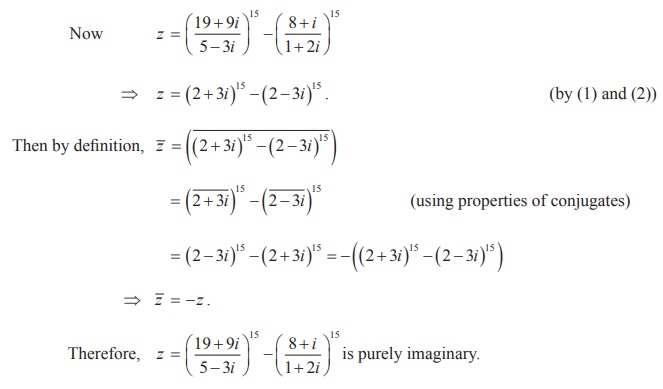
Related Topics