Chapter: 11th 12th std standard Class Physics sciense Higher secondary school College Notes
Bernoulli's theorem
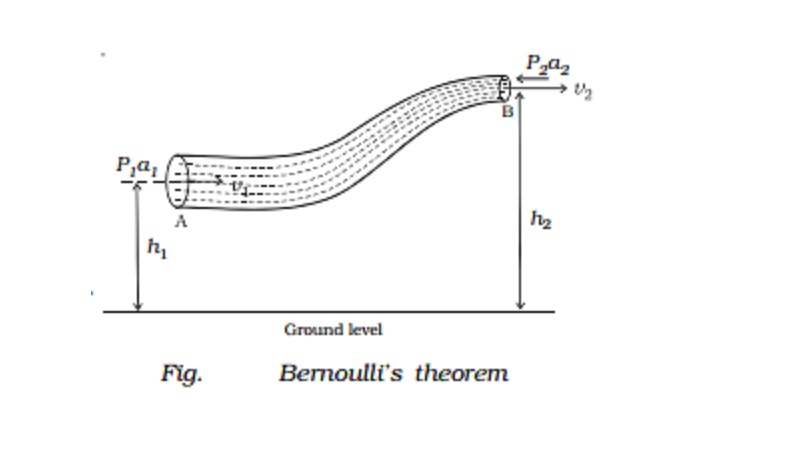
Bernoulli's theorem
In 1738, Daniel Bernoulli proposed a theorem for the streamline
flow of a liquid based on the law of conservation of energy. According to Bernoulli's
theorem, for the streamline flow of a non-viscous and incompressible liquid,
the sum of the pressure energy, kinetic energy and potential energy per unit
mass is a constant.
P/p + v2 +gh = constant.
This equation is known as Bernoulli's equation.
Consider streamline flow of a liquid of density
ñ through a pipe AB of varying cross section.
Let P1 and P2 be the pressures and a1 and a2, the cross sectional areas at A and B respectively.
The liquid enters A normally with a velocity v1 and leaves B normally with a velocity v2. The liquid is accelerated
against the force of gravity while flowing from A to B, because the height of B
is greater than that of A from the ground level. Therefore P1 is greater than P2.
This is maintained by an external force.
The mass m of the liquid
crossing per second through any section of the tube in accordance with the
equation of continuity is
a1v1ρ = a2v2ρ = m
or
a1v1 = a2v2 = m/p =V
As a1 > a2 , v1 < v2
The force acting on the liquid at A = P1a1
The force acting on the liquid at B = P2 a2
Work done per second on the liquid at A = P1a1
× v1 = P1V
Work done by the liquid at B = P2a2 × v2
= P2V
∴ Net work done per second on the
liquid by the pressure energy
in moving the liquid from A to B is = P1V - P2V
...(2)
If the mass of the liquid flowing in one second
from A to B is m, then increase in
potential energy per second of liquid from A to B is mgh2 - mgh1
Increase in kinetic energy per second of the
liquid
= ½ mv22 - ½ mv12
According to work-energy principle, work done
per second by the pressure energy = Increase in potential energy per second +
Increase in kinetic energy per second
P/p + gh + ½ v2 = constant
This is Bernoulli's equation. Thus the total
energy of unit mass of liquid remains constant.
Dividing equation (3) by g, p/pg + v2/2g
+ h = constant
Each term in this equation has the dimension of
length and hence is called head. p/pg is called pressure head, v2/2g
is velocity head and h is the gravitational head.
Special case :
If the liquid flows through a horizontal tube, h1 = h2.
Therefore there is no increase in potential energy of the liquid i.e. the
gravitational head becomes zero.
equation (3) becomes
P/p + 1/2v2 = a constant
This is another form of Bernoulli's equation.
Application of Bernoulli's
theorem
(i) Lift of an aircraft wing
A section of an aircraft wing and the flow lines are shown in Fig.
The orientation of the wing relative to the flow direction causes the flow
lines to crowd together above the wing. This corresponds to increased velocity
in this region and hence the pressure is
reduced. But below the wing, the pressure is nearly equal to the atmospheric
pressure. As a result of this, the upward force on the underside of the wing is
greater than the downward force on the topside. Thus there is a net upward
force or lift.
(ii) Blowing of roofs
During a storm, the roofs of huts or tinned roofs are blown off
without any damage to other parts of the hut. The blowing wind creates a low
pressure P1 on top of the roof. The pressure P2 under the
roof is however greater than P1. Due to this pressure difference,
the roof is lifted and blown off with
the wind.
(iii) Bunsen burner
In a Bunsen burner, the gas comes out of the nozzle with high
velocity. Due to this the pressure in the stem of the burner decreases. So, air
from the atmosphere rushes into the burner.
(iv) Motion of two parallel
boats
When two boats separated by a small distance row parallel to each
other along the same direction, the velocity of water between the boats becomes
very large compared to that on the outer sides. Because of this, the pressure
in between the two boats gets reduced. The high pressure on the outer side
pushes the boats inwards. As a result of this, the boats come closer and may
even collide.
Related Topics